Czym są funkcje trygonometryczne, po co one istnieją i jak je wyliczać na poszczególnych przykładach? Funkcje trygonometryczne z których korzystamy w trygonometrii na poziomie szkolnym to sinus (\(sin\)), cosinus (\(cos\)) oraz tangens (\(tg\)). Choć każda z tych funkcji jest nieco inna, to łączy je wspólny cel – każda z tych funkcji pokazuje nam jaki jest stosunek długości boków trójkąta prostokątnego względem jego miar kątów wewnętrznych.
Zastosowanie funkcji trygonometrycznych
Zanim powiemy sobie o tych funkcjach, to dobrze jest zrozumieć ich ideę. Załóżmy, że mamy trójkąt prostokątny i chcemy policzyć jego obwód. W początkowych klasach szkoły podstawowej aby tego dokonać to musieliśmy mieć podane wszystkie trzy długości boków. Z czasem kiedy poznaliśmy Twierdzenie Pitagorasa to się okazało, że wystarczy nam znajomość dwóch boków takiego trójkąta, bo trzeci jesteśmy w stanie sobie samodzielnie wyliczyć. Funkcje trygonometryczne pozwolą nam poznać wszystkie boki trójkąta mając dane np. tylko jeden bok oraz miarę jednego z kątów. Jakby tego było mało, to teraz będziemy w stanie podawać różne miary kątów w naszych trójkątach, znając jedynie poszczególne długości boków – to jest coś, czego do tej pory robić nie potrafiliśmy.
Można więc powiedzieć, że funkcje trygonometryczne wiążą nam ze sobą informacje na temat długości boków oraz miar kątów. Sprawdźmy zatem jak wyglądają interesujące nas funkcje i jak z nich korzystać:
Sinus jest funkcją, która bada stosunek długości przyprostokątnej leżącej naprzeciwko kąta \(α\) oraz długości przeciwprostokątnej. Możemy zapisać, że:
$$sinα=\frac{\text{dł. przyprostokątnej naprzeciw kąta α}}{\text{dł. przeciwprostokątnej}}$$
Zobaczmy jak to będzie wyglądać na przykładzie jakiegoś trójkąta:
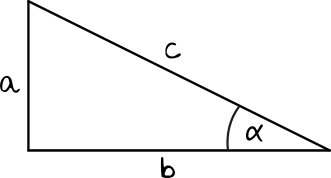
Stosując oznaczenia z rysunku możemy zapisać, że w tym konkretnym przypadku przyprostokątną leżącą naprzeciw kąta \(α\) jest bok \(a\), natomiast przeciwprostokątną jest bok \(c\). W związku z tym:
$$sinα=\frac{a}{c}$$
Od razu musimy sobie zaznaczyć, że nie jest dobrym pomysłem zapamiętanie regułki bazującej na oznaczeniach, czyli że \(sinα=\frac{a}{c}\), bo nasz trójkąt może mieć dowolne oznaczenia, może być dowolnie obrócony, a i nawet może być tak, że to ten drugi kąt ostry będzie oznaczony jako \(α\). Dużo lepszym sposobem jest zapamiętanie, że sinus to stosunek długości przeciwprostokątnej naprzeciw zaznaczonego kąta oraz długości przeciwprostokątnej. Aby zrozumieć dlaczego to jest tak istotne, to spójrzmy na poniższy przykład:
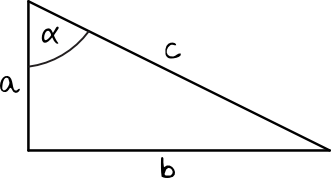
To jest dokładnie ten sam trójkąt co w pierwszym przykładzie, ale tym razem kątem \(α\) jest zupełnie inny kąt ostry. Gdybyśmy teraz zapisali, że sinus jest równy stosunkowi boku \(a\) oraz \(c\) to popełnilibyśmy błąd! Zasada cały czas jest ta sama – patrzymy jaki bok leży naprzeciwko kąta \(α\) i jaka jest przeciwprostokątna. Zatem w tej sytuacji:
$$sinα=\frac{b}{c}$$
Bardzo ważne jest aby zrozumieć różnice między pierwszym i drugim przykładem. Zły wybór długości boków to jest źródło najczęściej popełnianych błędów.
Cosinus jest to stosunek długości przyprostokątnej leżącej przy kącie alfa oraz długości przeciwprostokątnej.
$$cosα=\frac{\text{dł. przyprostokątnej przy kącie α}}{\text{dł. przeciwprostokątnej}}$$
Spróbujmy teraz zapisać czym jest cosinus w poniższym trójkącie:
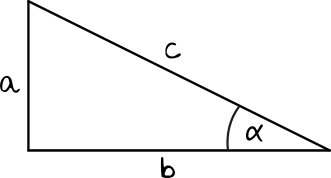
W tym trójkącie przyprostokątną przy kącie \(α\) jest bok \(b\), a przeciwprostokątną jest bok \(c\), zatem:
$$cosα=\frac{b}{c}$$
Teraz spójrzmy na taką sytuację:
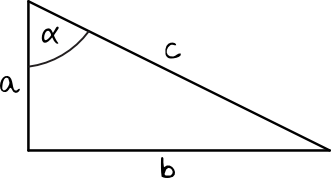
Analogicznie jak to było przy sinusie, tak i tutaj mamy najlepszy dowód na to, że nie warto uczyć się symboli jako takich, tylko trzeba znać poprawne zależności. Tym razem kąt \(α\) znalazł się w innym miejscu, przez co przyprostokątną przy kącie \(α\) jest tym razem bok \(a\). To oznacza, że w tym drugim przypadku:
$$cosα=\frac{a}{c}$$
Tangens to stosunek przyprostokątnej leżącej naprzeciwko kąta \(α\) oraz przyprostokątnej leżącej przy kącie \(α\).
$$tgα=\frac{\text{dł. przyprostokątnej naprzeciw kąta α}}{\text{dł. przyprostokątnej przy kącie α}}$$
Spójrzmy na poniższy rysunek:
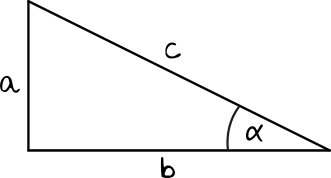
Przyprostokątną leżącą naprzeciw kąta \(α\) jest bok o długości \(a\), natomiast przyprostokątną przy kącie \(α\) jest bok \(b\), czyli w tym trójkącie:
$$tgα=\frac{a}{b}$$
Spróbujmy teraz określić wartość tangensa dla poniższego trójkąta:
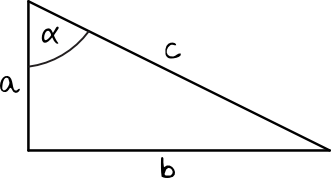
I tu podobnie jak to miało miejsce przy sinusie i cosinusie musimy zwracać uwagę na położenie tego kąta \(α\). W tym przypadku:
$$tgα=\frac{b}{a}$$
Z tangensem związana jest jego inna własność, która jest bardzo często wykorzystywana w zadaniach z trygonometrii. Okazuje się, że:
$$tgα=\frac{sinα}{cosα}$$
Warto o tym pamiętać, bo ta wiedza przydaje się np. w zadaniach na dowodzenie.
$$sinα=\frac{\text{dł. przyprostokątnej naprzeciw kąta α}}{\text{dł. przeciwprostokątnej}} \\
cosα=\frac{\text{dł. przyprostokątnej przy kącie α}}{\text{dł. przeciwprostokątnej}} \\
tgα=\frac{\text{dł. przyprostokątnej naprzeciw kąta α}}{\text{dł. przyprostokątnej przy kącie α}} \\
tgα=\frac{sinα}{cosα}$$
W takim razie skoro mamy omówione funkcje trygonometryczne to zróbmy sobie teraz przykłady na jakichś liczbach i przy okazji zobaczymy co nam z takich funkcji trygonometrycznych może wyjść.
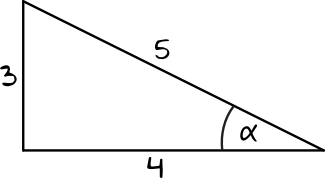
Na początek musimy obliczyć sinus kąta \(α\), czyli stosunek długości przyprostokątnej leżącej naprzeciwko kąta \(α\) oraz długości przeciwprostokątnej. Interesują nas więc tylko boki o długości \(3\) oraz \(5\). W związku z tym możemy zapisać, że:
$$sinα=\frac{3}{5}$$
Teraz obliczmy dla tego samego trójkąta wartość cosinusa kąta \(α\). Tym razem interesuje nas stosunek długości przyprostokątnej leżącej przy kącie \(α\) oraz przeciwprostokątnej. To oznacza, że:
$$cosα=\frac{4}{5}$$
Na koniec został nam do policzenia tangens. Zgodnie z naszą wiedzą, tangens jest stosunkiem długości przeciwprostokątnej leżącej naprzeciwko kąta \(α\) oraz przyprostokątnej leżącej przy tym kącie, zatem:
$$tgα=\frac{3}{4}$$
Przy okazji możemy sprawdzić jak działa ten drugi wzór na tangensa, czyli \(tgα=\frac{sinα}{cosα}\). Obliczyliśmy powyżej, że \(sinα=\frac{3}{5}\) oraz \(cosα=\frac{4}{5}\), a to oznacza, że tangens będzie równy:
$$tgα=\frac{sinα}{cosα} \\
tgα=\frac{\frac{3}{5}}{\frac{4}{5}} \\
tgα=\frac{3}{5}\cdot\frac{5}{4} \\
tgα=\frac{3}{4}$$

Mamy dokładnie ten sam trójkąt co powyżej, ale tym razem odnosimy się do drugiego kąta ostrego. Zacznijmy od sinusa. Przyprostokątną leżącą naprzeciwko kąta \(β\) jest bok o długości \(4\). Przeciwprostokątna ma długość \(5\). W związku z tym:
$$sinβ=\frac{4}{5}$$
Teraz cosinus. Przyprostokątna przy kącie ma długość \(3\), przeciwprostokątna ma długość \(5\), zatem:
$$cosβ=\frac{3}{5}$$
I na koniec tangens, czyli stosunek przyprostokątnej leżącej naprzeciwko kąta \(β\), która ma długość \(4\) oraz przyprostokątnej leżącej przy kącie, która ma długość \(3\). Zatem:
$$tgα=\frac{4}{3}$$
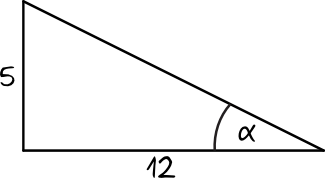
Tym razem musimy obliczyć wartość cosinusa i zgodnie z definicją wiemy, że interesuje nas przyprostokątna przy kącie \(α\) oraz przeciwprostokątna. Problemem w tym zadaniu jest fakt, że nie znamy długości przeciwprostokątnej. Bardzo często w różnych zadaniach będzie nam brakować jakiejś długości, ale z pomocą przyjdzie nam Twierdzenie Pitagorasa. Warto pamiętać, że Twierdzenie Pitagorasa bardzo często będzie tworzyć zgraną parę z funkcjami trygonometrycznymi.
$$a^2+b^2=c^2 \\
5^2+12^2=c^2 \\
25+144=c^2 \\
c^2=169 \\
c=13 \quad\lor\quad c=-13$$
Wartość ujemną oczywiście odrzucamy, bo bok nie może mieć ujemnej długości. Zostaje nam zatem \(c=13\). Teraz możemy przejść do obliczenia wartości cosinusa. Przyprostokątna przy kącie \(α\) ma długość \(12\), natomiast przeciwprostokątna ma długość \(13\), zatem:
$$cosα=\frac{12}{13}$$
Wartości przyjmowane przez sinus, cosinus oraz tangens
Umiemy już rozwiązywać podstawowe zadania, ale jeszcze dwa słowa powiedzmy sobie o otrzymanych wynikach. Okazuje się, że funkcje sinus oraz cosinus przyjmują zawsze wartości z przedziału \(\langle-1;1\rangle\). Nie ma zatem takiej możliwości, by sinus wyszedł nam równy np. \(2\). To bardzo ważna uwaga, bo pozwala nam ona wyłapać ewentualne błędy podczas obliczeń. Gdyby się np. okazało, że wyszedłby nam ułamek większy od \(1\), to mielibyśmy jasny sygnał, nam że musimy coś w swoich obliczeniach poprawić. My na matematyce w szkole (zwłaszcza na poziomie podstawowym) posługujemy się głównie kątami ostrymi w trójkącie prostokątnym i tu też warto zapamiętać, że dla kątów ostrych sinus oraz cosinus przyjmują wartości z przedziału \((0;1)\). Ta wiedza przyda nam się zwłaszcza przy rozwiązywaniu nieco trudniejszych zadań, gdzie będziemy musieli odrzucać ujemne rozwiązania właśnie ze względu na tę regułę. Tangens może przyjmować bardzo różne wartości, zarówno mniejsze od \(-1\), jak i większe od \(1\), tak więc tutaj nie sprawdzimy już tak łatwo poprawności naszych obliczeń.
Powiedzmy jeszcze sobie co nam daje wiedza o tym, że \(sinα\) jest równy np. \(\frac{3}{5}\). Ta informacja może się nam przydać do niektórych wzorów np. na pole powierzchni, ale przede wszystkim z wartości takiego sinusa (czy też innej funkcji trygonometrycznej) możemy odczytać miarę naszego kąta \(α\). Miary kątów odczytujemy z tablic, a o tym jak to się robi przeczytasz tutaj:

jasne wytłumaczenia i dobre przekłady.
Czy w tangensie (objaśnianiu) nie powinien pojawić się odwrotny stosunek?
Wszystko jest dobrze – zawsze bierzemy stosunek przyprostokątnej leżącej naprzeciwko kąta do przyprostokątnej leżącej przy kącie :)
Powiem tak,z matematyką mam spore trudności jednak tutaj mogę sobie dokładnie wszystko przejrzeć…dziękuje bardzo za prace w to włożoną ;D
Wszystko świetnie wyjaśnione, nie to co w tych książkach od matematyki! Pozdrawiam
Dziękuję za duży wkład pracy w wyjaśnieniu prostym językiem zasad trygonometrii. W szkole tak nie uczą.
kocham kogos kto to zrobil, giga mi to pomoglo, dziekuje! <3