Może się zdarzyć, że wartość bezwzględna pojawi nam się w nierówności. Taką nierównością będzie chociażby \(|x|\lt5\) czy też \(|x-3|\lt7\). Jak takie nierówności rozwiązać?
Aby dobrze zrozumieć istotę takich nierówności, wróćmy do początku wiedzy o wartości bezwzględnej. Mówiliśmy sobie, że wartość bezwzględna informuje nas od odległości danej liczby od zera na osi liczbowej. Z tego też względu zarówno \(|5|=5\) jak i \(|-5|=5\), bo i od „piątki” i od „minus piątki” mamy pięć jednostek na osi liczbowej do zera.
To teraz zastanówmy się, jakie liczby spełniają nierówność \(|x|\lt5\). Bazując na tym, co powiedzieliśmy przed chwilą – odległość niewiadomej \(x\) od zera musi być mniejsza niż \(5\) jednostek. Czyli pasowałby nam np. \(x=2\) czy też \(x=-4\), ale nie pasowałby nam \(x=8\) czy też \(x=-11\). Gdybyśmy chcieli przedstawić na osi liczbowej jakie wartości niewiadomej \(x\) spełniają tę nierówność, to wyglądałoby to w ten sposób:
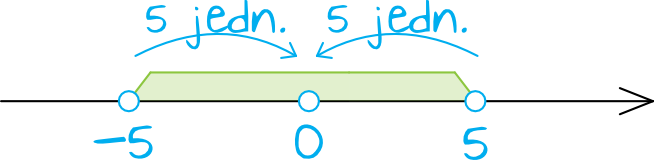
Na podstawie tego rysunku powinniśmy zauważyć, że rozwiązaniem nierówności \(|x|\lt5\) będzie przedział \(x\in(-5;5)\). To oznacza, że nierówność \(|x|\lt5\) będzie prawdziwa tylko wtedy, gdy pod \(x\) podstawimy dowolną liczbę większą od \(-5\) i jednocześnie mniejszą od \(5\).
Metoda rozwiązywania nierówności z wartością bezwzględną
Chcąc nie chcąc, rozwiązaliśmy już pierwszą nierówność z wartością bezwzględną, gdyż powyższa metoda graficzna jest oczywiście dobra i skuteczna. Jednak nie ma co się oszukiwać – nie zastosujemy tej metody przy bardziej rozbudowanych przykładach. Poznajmy więc bardziej uniwersalną metodę, która wynika tak naprawdę z tego co robiliśmy przed chwilą.
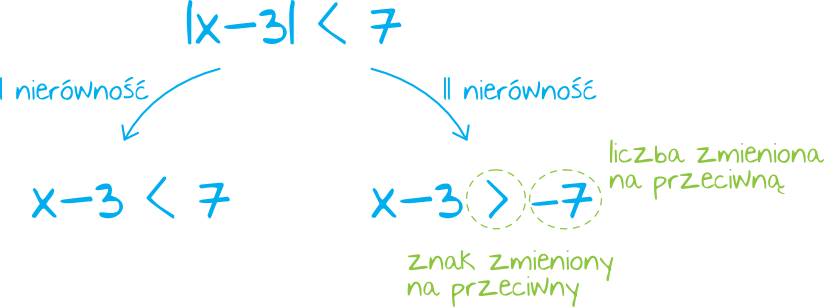
Załóżmy, że chcemy rozwiązać nierówność \(|x-3|\lt7\). Metoda rozwiązywania takich przykładów opiera się na ułożeniu dwóch nierówności:
I nierówność – jest identyczna jak ta początkowa, tyle tylko, że pomijamy znak wartości bezwzględnej.
II nierówność – pozbywając się znaku wartości bezwzględnej musimy zmienić znak nierówności na przeciwny, a także musimy zmienić na przeciwny znak liczby znajdującej się po prawej stronie.
W związku z tym w naszym przykładzie pierwszą nierównością byłoby \(x-3\lt7\), natomiast drugą \(x-3\gt-7\).
Teraz musimy te dwie nierówności rozwiązać, zatem:
$$x-3\lt7 \quad\quad\quad\quad\quad x-3\gt-7 \\
x\lt10 \quad\quad\quad\quad\quad x\gt-4$$
Otrzymaliśmy informację, że nasz \(x\) musi być mniejszy od \(10\), ale jednocześnie większy od \(-4\). To oznacza, że w takim razie rozwiązaniem nierówności \(|x-3|\lt7\) będzie przedział \(x\in(-4;10)\). Obrazowo rzecz ujmując możemy powiedzieć, że \(|x-3|\) będzie mniejsze od \(7\) tylko wtedy, gdy pod \(x\) podstawimy dowolną liczbę większą od \(-4\) i jednocześnie mniejszą od \(10\).
Korzystając ze zdobytej wiedzy, spróbujmy rozwiązać kilka przykładów nierówności z wartością bezwzględną:
Rozwiązanie:
Mamy klasyczną nierówność z wartością bezwzględną po lewej stronie. Musimy więc ułożyć dwie nierówności. Pierwsza nierówność jest bardzo prosta – przepisujemy nierówność bez wartości bezwzględnej. W drugiej nierówności, pozbywając się wartości bezwzględnej, musimy zmienić znak nierówności oraz liczbę stojącą po prawej stronie na przeciwną. Otrzymamy zatem:
$$2x-5\le3 \quad\quad\quad\quad\quad 2x-5\ge-3 \\
2x\le8 \quad\quad\quad\quad\quad 2x\ge2 \\
x\le4 \quad\quad\quad\quad\quad x\ge1$$
Obrazowo rzecz ujmując – wyszło nam, że \(x\) musi większy lub równy \(1\) ale jednocześnie mniejszy lub równy \(4\). To oznacza, że \(x\in\langle1;4\rangle\).
Rozwiązanie:
Przykład niemal identyczny jak przed chwilą, tylko znak nierówności jest inny. Niczego to nie zmienia w naszym postępowaniu, zatem ponownie usuwamy wartość bezwzględną z zapisu i zapisujemy dwie nierówności (pamiętając o tym, by przy drugiej nierówności zmienić znak oraz liczbę na przeciwne).
$$2x-5\gt3 \quad\quad\quad\quad\quad 2x-5\lt-3 \\
2x\gt8 \quad\quad\quad\quad\quad 2x\lt2 \\
x\gt4 \quad\quad\quad\quad\quad x\lt1$$
Tym razem nasz \(x\) może być mniejszy od \(1\) oraz większy od \(4\), zatem \(x\in(-\infty;1)\cup(4;+\infty)\).
Rozwiązanie:
Aby rozwiązać tę nierówność, musimy doprowadzić do sytuacji, w której po lewej stronie będziemy mieć wartość bezwzględną, a po prawej liczbę. Dzieląc zatem obydwie strony nierówności przez \(2\), otrzymamy:
$$2\cdot|x-4|\lt-10 \quad\bigg/:2 \\
|x-4|\lt-5$$
I teraz zastanówmy się – czy jest możliwe, by wartość bezwzględna \(|x-4|\) była mniejsza niż \(-5\)? Taka sytuacja jest niemożliwa, wartość bezwzględna jest zawsze dodatnia. Stąd też ta nierówność nie ma rozwiązań.
Rozwiązanie:
Z pozoru przykład wydaje się nieco trudniejszy, gdyż wartość bezwzględna ukryta jest w liczniku ułamka. To w żaden sposób nie zmienia naszej strategii rozwiązywania, zatem doprowadzamy do sytuacji, w której po lewej stronie mamy jedynie wartość bezwzględną:
$$\frac{|2x|-4}{2}\le5 \quad\bigg/\cdot2 \\
|2x|-4\le10 \\
|2x|\le14$$
Teraz możemy przystąpić do pozbycia się wartości bezwzględnej i zapisania naszych dwóch nierówności:
$$2x\le14 \quad\quad\quad\quad\quad 2x\ge-14 \\
x\le7 \quad\quad\quad\quad\quad x\ge-7$$
Możemy więc zapisać, że \(x\in\langle-7;7\rangle\).
Rozwiązanie:
To zdecydowanie najtrudniejszy przykład i trzeba być tutaj naprawdę ostrożnym. Cały czas chcemy doprowadzić do sytuacji, w której po lewej stronie mamy jedynie wartość bezwzględną, a więc najpierw odejmiemy obustronnie \(4\):
$$4-2\cdot|x-4|\gt-10 \quad\bigg/-4 \\
-2\cdot|x-4|\gt-14$$
I tutaj mamy największą pułapkę występującą w tego typu zadaniach. Musimy teraz podzielić obie strony przez liczbę ujemną (czyli przez \(-2\)). Z działu nierówności powinniśmy pamiętać, że mnożąc lub dzieląc nierówność przez liczbę ujemną, musimy zmienić znak na przeciwny. W związku z tym:
$$-2\cdot|x-4|\gt-14 \quad\bigg/:(-2) \\
|x-4|\lt7$$
Wszystkie trudności już pokonane, więc możemy standardowo zapisać nasze dwie nierówności:
$$x-4\lt7 \quad\quad\quad\quad\quad x-4\gt-7 \\
x\lt11 \quad\quad\quad\quad\quad x\gt-3$$
To oznacza, że \(x\in(-3;11)\).
Może się też zdarzyć sytuacja, w której nierówność damy radę rozwiązać bez rozpisywania danego przykładu. Mowa tutaj przede wszystkim i przypadkach, gdzie rozwiązaniem nierówności będzie zbiór liczb rzeczywistych lub zbiór pusty.
Rozwiązanie:
W tym przykładzie nie musimy wykonywać jakichkolwiek obliczeń. Wartość bezwzględna jest zawsze większa lub równa \(0\), więc jej rozwiązaniem będzie zbiór liczb rzeczywistych, czyli \(x\in\mathbb{R}\). Mówiąc wprost – możemy do nierówności podstawić dowolną liczbę i zawsze prawa strona będzie równa stronie prawej.
Rozwiązanie:
Analogicznie jak przed chwilą – skoro wartość bezwzględna jest zawsze dodatnia lub równa zero, to nie ma możliwości, by lewa strona była mniejsza od zera. Rozwiązaniem tej nierówności jest wiec zbiór pusty, czyli \(x\in\emptyset\).
Tutaj musimy być ostrożni, gdyż podejście do tej nierówności będzie dość nietypowe. Na pewno z wartości bezwzględnej nie otrzymamy liczby, która jest mniejsza od zera. Jest jednak możliwe to, że ta wartość będzie równa zero i ten wariant musimy rozpatrzeć (bo w nierówności mamy \(\le0\)). Całość sprowadzi się więc do tego, że musimy sprawdzić kiedy \(3x-6\) jest równe \(0\). Można więc powiedzieć, że w tej wyjątkowej sytuacji, do rozwiązania nierówności doprowadzi nas pojedyncze równanie:
$$3x-6=0 \\
3x=6 \\
x=2$$
To oznacza, że rozwiązaniem całej nierówności będzie \(x=2\).
