Rozwiązanie
Krok 1. Ustalenie liczby krawędzi sześcianu i czworościanu.
Budując bryły z patyczków budujemy tak naprawdę szkielet w którym patyczki są krawędziami danej bryły. Chcąc więc zacząć rozwiązywanie tego zadania musimy w ogóle ustalić ile krawędzi mają poszczególne bryły:
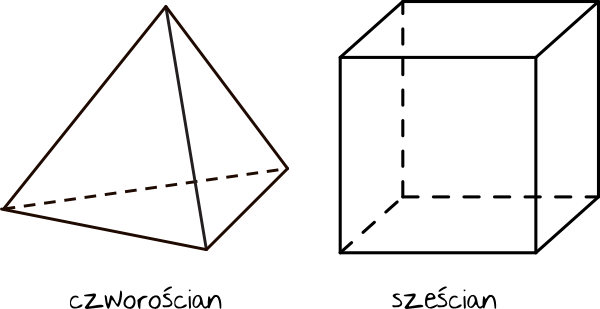
Czworościan ma \(6\) krawędzi, a sześcian ma \(12\) krawędzi.
Krok 2. Zapisanie prawidłowego układu równań.
Pierwsze równanie jest tak naprawdę znane, nawet przyglądając się wszystkim odpowiedziom widzimy wyraźnie, że w każdej z odpowiedzi pojawia się \(x+y=15\). Jest to logiczne, bo wszystkich brył ma być dokładnie \(15\). Ustalmy zatem jakie będzie drugie równanie. Skoro na każdy czworościan zużywamy \(6\) patyczków, to na \(x\) czworościanów zużyjemy \(6x\) patyczków. Analogicznie skoro na każdy sześcian zużywamy \(12\) patyczków, to na \(y\) sześcianów zużyjemy \(12y\) patyczków. Łącznie patyczków mamy \(120\), zatem drugim równaniem będzie na pewno:
$$6x+12y=120$$
To oznacza, że prawidłowy układ równań jest zapisany w czwartej odpowiedzi.