Notacja wykładnicza to uproszczona forma zapisu bardzo dużych lub bardzo małych liczb. Zobaczmy zatem na czym to uproszczenie polega i w jaki sposób będziemy z niego korzystać.
Przykładem notacji wykładniczej jest zapis \(3\cdot10^5\). Spróbujmy odkryć jaka to liczba kryje się pod takim działaniem. Nie jest to trudne, bo wystarczy wykonać mnożenie:
$$3\cdot10^5=3\cdot10\cdot10\cdot10\cdot10\cdot10=300\;000$$
Udało nam się w ten sposób pokazać, że liczba \(300\;000\) to jest dokładnie to samo co \(3\cdot10^5\). Widzimy więc wyraźnie, że główną (choć nie jedyną) ideą notacji wykładniczej jest pozbycie się z zapisu zer i zapisanie wszystkiego w formie dziesiątki podniesionej do jakiejś potęgi. Stąd też postać notacji wykładniczej możemy zapisać jako \(a\cdot10^n\), gdzie:
\(1\le a\lt10\)
\(n\) – liczba całkowita
Dobrze, to teraz spróbujmy w drugą stronę – mamy jakąś dużą liczbę i chcemy ją zapisać w notacji wykładniczej. Jak tego dokonać? Spójrzmy na poniższy przykład:
Najbardziej niezawodną zapisywania notacji wykładniczej jest metoda związana z przesuwaniem przecinków. W przypadku liczb całkowitych traktujemy sytuację tak, jakby przecinek stał na końcu tej liczby, czyli tak jakby to było coś w stylu \(4\;000\;000,\). Teraz przesuwamy ten przecinek w taki sposób, aby powstała nam liczba większa lub równa 1 i mniejsza od 10. W naszej sytuacji musimy przesunąć ten przecinek aż do czwórki, otrzymując liczbę \(4,000000\) (czyli mieszczącą się w zakładanym przedziale). Całość wyglądać będzie w następujący sposób:
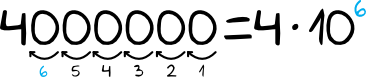
Widzimy, że liczba znajdująca się w potędze notacji wykładniczej jest równa liczbie przesunięć naszego przecinka i to będzie dla nas klucz do szybkiego i sprawnego zapisywania notacji wykładniczych. W ten sposób pokazaliśmy, że \(4\;000\;000=4\cdot10^6\).
Jest to bardzo podobny przykład, ale można tutaj nabrać wątpliwości jak daleko trzeba przesuwać przecinek – czy do jedynki, czy do czwórki. Spójrzmy zatem jak to powinno wyglądać:
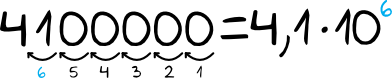
Przecinek przesunęliśmy najdalej jak się da (czyli do czwórki) otrzymując w ten sposób wynik \(4,1\cdot10^6\). A czy byłoby dużym błędem, gdybyśmy ten przecinek przesuwali tylko do jedynki, otrzymując w ten sposób zapis \(41\cdot10^5\)? Duży błąd to nie jest, ale jest to pewnego rodzaju nieścisłość, bowiem ustaliliśmy na początku że liczba która stoi przed potęgowaniem dziesiątki ma być większa lub równa \(1\) i mniejsza od \(10\). Dlatego też starajmy się zapisywać liczby w taki sposób, by otrzymywać jak najprostszy zapis.
W powyższych przykładach zamienialiśmy na notację wykładniczą duże liczby. Teraz zajmiemy się liczbami bardzo małymi, czyli takimi które mają dużo zer po przecinku.
Idea jest taka sama jak przed chwilą – przesuwamy przecinek w taki sposób, by otrzymać liczbę większą lub równą 1 i mniejszą niż 10. W tym konkretnym przypadku przecinek musimy więc przesunąć w prawą (a nie lewą stronę). I tu pojawia się główna różnica względem poprzednich przykładów, bowiem przesuwając przecinek w prawą stronę nasz wykładnik potęgi będzie ujemny:

Cały czas dążymy do tego, aby liczba stojąca przed potęgowaniem była większa lub równa \(1\) i mniejsza od \(10\), zatem przesunięcie przecinka wygląda następująco.
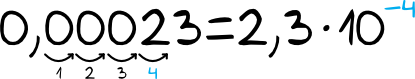
To na sam koniec omówmy jeszcze sytuację bardziej nietypową. Czy dałoby się zamienić na notację wykładniczą np. liczbę \(54321\)? Jest to możliwe, cały proces tworzenia taki zapisu jest dokładnie taki sam jak przed chwilą. Różnica jest tylko taka, że w tej sytuacji notacja wykładnicza niezbyt wiele nam uprości:
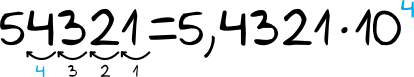
Można nawet powiedzieć, że otrzymany wynik jest mniej praktyczny i mniej poręczny niż zapis \(54321\), aczkolwiek mogą się zdarzyć szczególne sytuacje w których taka forma nam się przyda. Generalnie notacja wykładnicza jest najbardziej przydatna wtedy, kiedy mamy dużą liczbę zer. Z tego też względu czasem nawet stosuje się przybliżenia, aby móc zapisać coś w znacznie wygodniejszej formie. Przykładowo:
$$6\;513=6,513\cdot10^3\approx6,5\cdot10^3 \\
5\;000\;031=5,000031\cdot10^6\approx5\cdot10^6 \\
299\;792\;458=2,99792458\cdot10^8\approx3\cdot10^8$$

dzięki już rozumiem.
Super, dziękuje bardzo ❤️❤️