Bryły obrotowe – zadania maturalne

B

Objętość stożka wyliczymy ze wzoru \(V=\frac{1}{3}\cdot h\cdot π\cdot r^2\). Wszystkie dane tak naprawdę mamy podane w treści zadania, musimy tylko obliczyć długość promienia. Skoro średnica ma długość \(12\), to promień jest równy \(12:2=6\).

Teraz bez przeszkód obliczymy objętość naszej bryły:
$$V=\frac{1}{3}\cdot h\cdot π\cdot r^2 \\
V=\frac{1}{3}\cdot 8\cdot π\cdot 6^2 \\
V=\frac{1}{3}\cdot 8\cdot 36\cdot π \\
V=\frac{1}{3}\cdot288\cdot π \\
V=96π$$

A

Promień kuli wyznaczymy ze wzoru na jej objętość:
$$V=\frac{4}{3}πr^3 \\
288π=\frac{4}{3}πr^3 \quad\bigg/:π \\
288=\frac{4}{3}r^3 \quad\bigg/\cdot\frac{3}{4} \\
r^3=216 \\
r=6$$

A

Krok 1. Sporządzenie rysunku poglądowego.



Widzimy, że promień, wysokość oraz tworząca stożka utworzyły nam trójkąt prostokątny \(ABC\). Znamy tylko długość tworzącej stożka oraz miarę kąta jej nachylenia do podstawy, więc chcąc obliczyć wysokość stożka musimy skorzystać albo z własności trójkątów \(45°, 45°, 90°\) albo z trygonometrii.

Krok 2. Obliczenie wysokości stożka.
Korzystając z zasad trygonometrii otrzymamy:
$$sin45°=\frac{h}{l} \\
\frac{\sqrt{2}}{2}=\frac{h}{4} \\
h=2\sqrt{2}$$

B

Krok 1. Sporządzenie rysunku poglądowego.
Spróbujmy sobie narysować pożądany walec i zaznaczmy na nim poszczególne długości:



Widzimy wyraźnie, że prawdziwe będą dwie równości:
$$a=2r \\
a=h \\
\text{Zatem }2r=h$$

Krok 2. Wybór prawidłowego równania.
Sprawdźmy teraz po kolei które z równań jest zapisane poprawnie, podstawiając \(a=2r\) oraz \(h=2r\):
Odp. A.
\(r+h=a \\
r+2r=2r \\
3r=2r \\
L\neq P\)

Odp. B.
\(h-r=\frac{a}{2} \\
2r-r=\frac{2r}{2} \\
r=r \\
L=P\)

Odp. C.
\(r-h=\frac{a}{2} \\
r-2r=\frac{2r}{2} \\
-r=r \\
L\neq P\)

Odp. D.
\(r^2+h^2=a^2 \\
r^2+(2r)^2=(2r)^2 \\
r^2+4r^2=4r^2 \\
5r^2=4r^2 \\
L\neq P\)

Prawidłowa zależność znalazła się tylko w drugiej odpowiedzi.

D

Krok 1. Sporządzenie rysunku poglądowego.
Skoro w przekroju jest trójkąt równoboczny, to możemy wprowadzić następujące oznaczenia:



Z rysunku wynika, że promień podstawy jest równy \(r=\frac{1}{2}a\).

Krok 2. Wyznaczenie pola podstawy i wysokości stożka.
Znając długość promienia możemy obliczyć pole podstawy stożka:
$$P_{p}=πr^2 \\
P_{p}=π\cdot\left(\frac{1}{2}a\right)^2 \\
P_{p}=\frac{1}{4}πa^2$$

Wysokość stożka jest wysokością naszego trójkąta równobocznego, zatem zgodnie ze standardowym wzorem na wysokość trójkąta równobocznego:
$$H=\frac{a\sqrt{3}}{2}$$

Krok 3. Obliczenie objętości stożka.
Do wzoru na objętość stożka musimy podstawić dane wyznaczone w drugim kroku:
$$V=\frac{1}{3}P_{p}\cdot H \\
V=\frac{1}{3}\cdot\frac{1}{4}πa^2\cdot\frac{a\sqrt{3}}{2} \\
V=\frac{\sqrt{3}}{24}πa^3$$

C

Krok 1. Sporządzenie rysunku pomocniczego.



Znamy miarę \(h=4\) oraz \(r=3\). Nam jest potrzebna znajomość długość tzw. "tworzącej stożka" czyli \(l\), bo to dzięki niej wyliczymy pole powierzchni bocznej bryły. Skorzystamy tutaj oczywiście z Twierdzenia Pitagorasa.

Krok 2. Obliczenie długości tworzącej \(l\).
$$r^2+h^2=l^2 \\
l^2=3^2+4^2 \\
l^2=9+16 \\
l^2=25 \\
l=5 \quad\lor\quad l=-5$$

Ujemną wartość oczywiście odrzucamy, bo długość nie może być ujemna.

Krok 3. Obliczenie pola powierzchni bocznej stożka.
$$P_{b}=πrl=π\cdot3\cdot5=15π$$

D

Wzór na objętość stożka możemy zapisać jako:
$$V=\frac{1}{3}πr^2h$$

Skoro \(r=\frac{1}{3}h\), to:
$$V=\frac{1}{3}π\cdot\left(\frac{1}{3}h\right)^2\cdot h \\
V=\frac{1}{3}π\cdot\frac{1}{9}h^2\cdot h \\
V=\frac{1}{27}πh^3$$

D

Objętość walca obliczamy za pomocą następującego wzoru:
$$V=πr^2h$$

Znamy wartość \(h=8\), wiemy też, że \(V=72π\), tak więc bez problemu wyznaczymy z tego wzoru długość promienia podstawy:
$$72π=πr^2\cdot8 \\
r^2=9 \\
r=3$$

C

Pole powierzchni bocznej stożka możemy zapisać wzorem: \(πrl\)
Pole powierzchni bocznej walca możemy zapisać jako: \(2πrH\)
Skoro pola są sobie równe to:
$$πrl=2πrH \quad\bigg/:πr \\
l=2H$$

Z powyższej analizy wynika, że tworząca stożka jest dwa razy dłuższa od wysokości walca.

D

Krok 1. Wyznaczenie wysokości walca.
Do wyznaczenia pola powierzchni bocznej walca brakuje nam jego wysokości. Obliczymy ją korzystając ze wzoru na objętość:
$$V=πr^2H \\
96π=π\cdot4^2\cdot H \\
96π=16π\cdot H \\
H=6$$

Krok 2. Obliczenie pola powierzchni bocznej walca.
$$P_{b}=2πrH \\
P_{b}=2π\cdot4\cdot6 \\
P_{b}=48π$$

D

Krok 1. Obliczenie długości promienia walca oraz jego wysokości.
Skoro w przekroju osiowym walca jest kwadrat o boku \(4\), to promień podstawy będzie równy połowie tej długości, czyli \(r=2\).
Wysokość walca będzie równa długości boku tego kwadratu, czyli \(H=4\).



Krok 2. Obliczenie pola powierzchni całkowitej walca.
Pole powierzchni całkowitej walca obliczymy ze wzoru:
$$P_{c}=2πr^2+2πrH \\
P_{c}=2π\cdot2^2+2π\cdot2\cdot4 \\
P_{c}=2π\cdot4+2π\cdot8 \\
P_{c}=8π+16π \\
P_{c}=24π$$

B

Krok 1. Obliczenie długości \(r\) oraz \(h\).



Spójrzmy na rysunek szkicowy. Do obliczenia objętości będziemy potrzebować długości promienia oraz wysokości bryły. Skoro przekrój jest trójkątem równobocznym, to na pewno wysokość dzieli podstawę na dwie równe części, a to z kolei oznacza że \(r=6:2=3\).

Wysokość \(h\) także nie stanowi problemu, bo mamy w tablicach wzór na wysokość trójkąta równobocznego:
$$h=\frac{a\sqrt{3}}{2}=\frac{6\sqrt{3}}{2}=3\sqrt{3}$$

Gdybyśmy nie pamiętali o tym wzorze, to wysokość można byłoby obliczyć z Twierdzenia Pitagorasa.

Krok 2. Obliczenie objętości bryły.
Znamy długość promienia, znamy wysokość, więc podstawiając dane do wzoru obliczymy objętość stożka:
$$V=\frac{1}{3}πr^2h \\
V=\frac{1}{3}π\cdot3^2\cdot3\sqrt{3} \\
V=\frac{1}{3}π\cdot9\cdot3\sqrt{3} \\
V=3\cdot3\sqrt{3}π \\
V=9\sqrt{3}π$$

C

Musimy zauważyć, że w przekroju stożka znalazł się trójkąt równoboczny. Skąd to wiemy? Skoro promień stożka jest równy \(3\), to średnica (czyli de facto podstawa trójkąta) ma długość \(6\). Tworząca stożka (czyli ramiona trójkąta) ma także długość \(6\), a to oznacza, że wszystkie boki są jednakowej długości. Dostrzeżenie tej zależności pozwala nam powiedzieć, że kąt \(α=60°\), bowiem w trójkącie równobocznym wszystkie kąty mają miarę \(60°\).

D

Krok 1. Obliczenie objętości kuli.
$$V_{k}=\frac{4}{3}πR^3 \\
V_{k}=\frac{4}{3}π\cdot5^3 \\
V_{k}=\frac{4}{3}π\cdot125 \\
V_{k}=\frac{500}{3}π$$

Krok 2. Obliczenie objętości stożka.
$$V_{s}=\frac{1}{3}πr^2H \\
V_{s}=\frac{1}{3}π\cdot10^2\cdot H \\
V_{s}=\frac{1}{3}π\cdot100\cdot H \\
V_{s}=\frac{100}{3}π\cdot H$$

Krok 3. Obliczenie wysokości stożka.
We wzorze na objętość stożka znajdzie się wysokość \(H\), którą wyznaczymy sobie porównując do siebie objętości dwóch brył.
$$V_{k}=V_{s} \\
\frac{500}{3}π=\frac{100}{3}π\cdot H \quad\bigg/\cdot3 \\
500π=100π\cdot H \quad\bigg/:100π \\
H=5[cm]$$

D

Krok 1. Sporządzenie rysunku poglądowego.
Skoro kąt rozwarcia stożka ma miarę \(120°\), to znaczy że powstanie nam mniej więcej coś takiego:



Udało nam się wyodrębnić trójkąt prostokątny, tak więc znając miary poszczególnych kątów oraz znając miarę tworzącej stożka jesteśmy w stanie obliczyć wysokość i promień stożka przy użyciu funkcji trygonometrycznych. Możemy także skorzystać z własności trójkątów \(30°, 60°, 90°\).

Krok 2. Obliczenie długości promienia stożka.
Zgodnie z zasadami trygonometrii:
$$\frac{r}{4}=cos30° \\
\frac{r}{4}=\frac{\sqrt{3}}{2} \\
r=2\sqrt{3}$$

Krok 3. Obliczenie wysokości stożka.
Ponownie użyjemy funkcji trygonometrycznych, tym razem sinusa:
$$\frac{h}{4}=sin30° \\
\frac{h}{4}=\frac{1}{2} \\
h=2$$

Krok 4. Obliczenie objętości bryły.
Znając długość promienia podstawy oraz wysokość stożka możemy bez przeszkód obliczyć jego objętość:
$$V=\frac{1}{3}πr^2h \\
V=\frac{1}{3}π\cdot(2\sqrt{3})^2\cdot2 \\
V=\frac{1}{3}π\cdot4\cdot3\cdot2 \\
V=\frac{1}{3}π\cdot24 \\
V=8π$$

C

Spróbujmy stworzyć rysunek poglądowy:


Kiedy naniesiemy sobie wszystkie dane z treści zadania na szkic rysunku to okaże się, że tak naprawdę musimy obliczyć długość podstawy trójkąta prostokątnego. To oznacza, że będziemy mogli skorzystać z funkcji trygonometrycznych albo też z własności trójkątów \(30°,60°,90°\). Zatem:
$$\frac{r}{6}=sin60° \\
\frac{r}{6}=\frac{\sqrt{3}}{2} \\
r=3\sqrt{3}$$

A

Jeżeli promień podstawy jest równy \(r\) to wysokość walca możemy opisać jako \(2r\). Objętość tego walca jest więc równa:
$$V=πr^2h \\
V=πr^2\cdot2r \\
V=2πr^3$$

B

Krok 1. Sporządzenie rysunku poglądowego.
Skoro długość promienia podstawy oraz wysokość tego walca są sobie równe, to trójkąt \(SAO\) wygląda mniej więcej w ten sposób:



Naszym zadaniem jest wyznaczenie sinusa kąta \(α\). Tak naprawdę można byłoby na tym kroku zakończyć rozwiązywanie tego zadania, bo widzimy że jest to trójkąt równoramienny prostokątny, a więc kąt ostry musi mieć miarę \(α=45°\). Skoro tak, to możemy odczytać z tablic, że:
$$sin45°=\frac{\sqrt{2}}{2}$$

Gdybyśmy jednak nie dostrzegli tego, to można dotrzeć do tej wartości trochę dłuższym sposobem.

Krok 2. Wyznaczenie długości odcinka \(d\).
Już po samym rysunku widzimy, że odcinek \(d\) jest tak jakby przekątną kwadratu o boku długości \(r\), zatem na pewno \(d=r\sqrt{2}\). Gdybyśmy o tym nie pamiętali, to zawsze możemy się jeszcze ratować Twierdzeniem Pitagorasa:
$$r^2+r^2=d^2 \\
2r^2=d^2 \\
d=\sqrt{2r^2} \\
d=r\sqrt{2}$$

Krok 3. Wyznaczenie wartości sinusa kąta \(OAS\).
Zgodnie z własnościami funkcji trygonometrycznych:
$$\require{cancel}
sinα=\frac{r}{d} \\
sinα=\frac{\cancel{r}}{\cancel{r}\sqrt{2}} \\
sinα=\frac{1}{\sqrt{2}}=\frac{1\cdot\sqrt{2}}{\sqrt{2}\cdot\sqrt{2}}=\frac{\sqrt{2}}{2}$$

D

Do wzoru na objętość stożka potrzebujemy znać długość promienia podstawy. W treści zadania mamy podaną średnicę, zatem:
$$r=12:2=6$$

Teraz możemy podstawić wszystkie dane z treści zadania (\(r=6\), \(H=4\)) i obliczyć poszukiwaną objętość:
$$V=\frac{1}{3}πr^2 H \\
V=\frac{1}{3}π\cdot6^2\cdot4 \\
V=\frac{1}{3}π\cdot36\cdot4 \\
V=\frac{1}{3}π\cdot144 \\
V=48π$$

D

Krok 1. Ułożenie poprawnego równania na podstawie danych z treści zadania.
Skoro powierzchnia boczna stożka (określana wzorem \(πrl\)) jest \(2\) razy większa od pola podstawy (określanego wzorem \(πr^2\)), to znaczy że prawdziwe jest równanie:
$$πrl=2\cdot πr^2$$

(Mnożymy przez \(2\) pole podstawy by było one równe polu ściany bocznej.)

Krok 2. Wyznaczenie wartości \(r\).
Na podstawie zapisanego równania możemy wyznaczyć długość promienia \(r\), zatem:
$$πrl=2\cdot πr^2 \quad\bigg/:π \\
rl=2r^2 \quad\bigg/:r \\
l=2r \\
r=\frac{1}{2}l$$

\(P_{c}=480π\) oraz \(V=600π\)

Krok 1. Sporządzenie rysunku poglądowego.
Narysujmy sobie przekrój stożka i zaznaczmy na nim odpowiednie miary i oznaczenia:



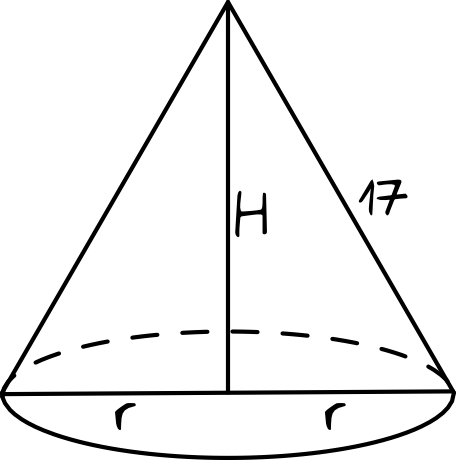
Warto sobie od razu zapisać, że zgodnie z treścią zadania wysokość stożka jest krótsza o \(22\) od średnicy podstawy (średnicy, nie promienia!). Zatem:
$$H=2r-22$$

Krok 2. Wyznaczenie długości promienia podstawy.
Możemy skorzystać z Twierdzenia Pitagorasa, podstawiając za wysokość \(H=2r-22\). Otrzymamy wtedy:
$$r^2+H^2=17^2 \\
r^2+(2r-22)^2=289 \\
r^2+4r^2-88r+484=289 \\
5r^2-88r+195=0$$

Krok 3. Rozwiązanie powstałego równania kwadratowego.
Współczynniki: \(a=5,\;b=-88,\;c=195\)
$$Δ=b^2-4ac=(-88)^2-4\cdot5\cdot195=7744-3900=3844 \\
\sqrt{Δ}=\sqrt{3844}=62$$

$$r_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-(-88)-62}{2\cdot5}=\frac{88-62}{10}=\frac{26}{10}=2,6 \\
r_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-(-88)+62}{2\cdot5}=\frac{88+62}{10}=\frac{150}{10}=15$$

Obydwa rozwiązania są póki co dobre, żadnego z nich nie możemy odrzucić (odrzucilibyśmy np. wtedy, gdyby któraś z wartości wyszła ujemna).

Krok 4. Obliczenie wysokości stożka.
Jeśli \(r_{1}=2,6\), to \(H_{1}=2\cdot2,6-22=5,2-22=-16,8\)
Jeśli \(r_{2}=15\), to \(H_{2}=2\cdot15-22=30-22=8\)

W przypadku pierwszej pary wyszła nam ujemna wysokość, więc odrzucamy całe to rozwiązanie. To oznacza, że jest tylko jedna para liczb, która spełnia warunki naszego zadania: \(r=15\) oraz \(H=8\).

Krok 5. Obliczenie objętości stożka.
Znając promień podstawy i wysokość stożka możemy już bez problemu obliczyć jego objętość:
$$V=\frac{1}{3}πr^2 H \\
V=\frac{1}{3}\cdot15^2\cdot8π \\
V=\frac{1}{3}\cdot225\cdot8π \\
V=\frac{1}{3}\cdot1800π \\
V=600π$$

Krok 6. Obliczenie pola powierzchni całkowitej.
Zgodnie z treścią zadania musimy jeszcze obliczyć pole powierzchni całkowitej.
$$P_{c}=πr\cdot(r+l) \\
P_{c}=π\cdot15\cdot(15+17) \\
P_{c}=π\cdot15\cdot32 \\
P_{c}=480π$$

Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy zapiszesz równanie wynikające z Twierdzenia Pitagorasa i doprowadzisz je do postaci w której jedyną niewiadomą jest długość promienia (patrz: Krok 2.).
2 pkt
• Gdy rozwiążesz powstałe równanie kwadratowe (patrz: Krok 3.).
3 pkt
• Gdy obliczysz, że \(r=15\) oraz \(H=8\) (patrz: Krok 4.).
ALBO
• Gdy rozwiążesz całe zadanie, ale zapomnisz obliczyć pole powierzchni całkowitej (patrz: Krok 6.).
4 pkt
• Gdy otrzymasz oczekiwany wynik.

\(P_{b}=2\sqrt{73}π\)

Krok 1. Sporządzenie rysunku poglądowego.



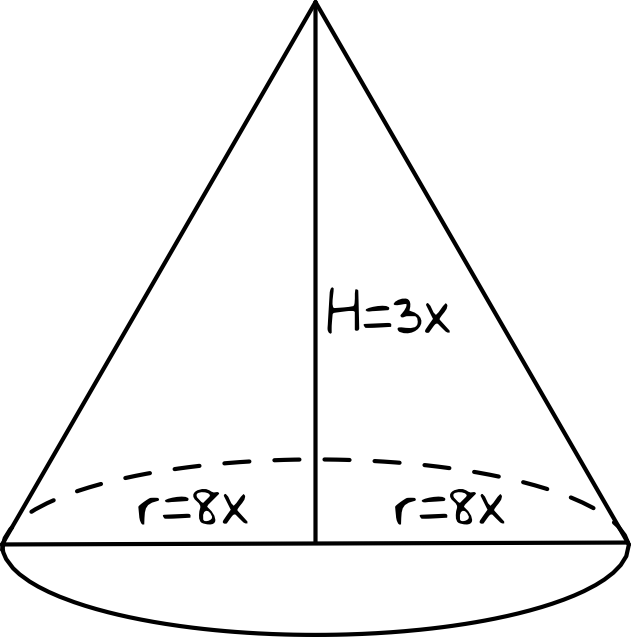
Oprócz naszkicowania sobie bryły wprowadźmy też oznaczenia, które pozwolą nam odnieść się do stosunku wysokości do promienia podstawy. Niech więc wysokość stożka będzie równa \(3x\), a promień podstawy \(8x\). Możemy też zapisać, że \(\frac{H}{r}=\frac{3}{8}\).

Krok 2. Obliczenie wartości \(x\).
Skorzystamy tutaj ze wzoru na objętość stożka.
$$V=\frac{1}{3}πr^2\cdot H \\
8π=\frac{1}{3}π\cdot(8x)^2\cdot3x \\
8π=\frac{1}{3}π\cdot64x^2\cdot3x \\
8=64x^3 \\
x^3=\frac{1}{8} \\
x=\frac{1}{2}$$

To oznacza, że:
$$r=8x=8\cdot\frac{1}{2}=4 \\
H=3x=3\cdot\frac{1}{2}=\frac{3}{2}$$

Krok 3. Obliczenie długości tworzącej stożka.
Skorzystamy tutaj z Twierdzenia Pitagorasa:
$$r^2+H^2=l^2 \\
4^2+\left(\frac{3}{2}\right)^2=l^2 \\
16+\frac{9}{4}=l^2 \\
l^2=\frac{64}{4}+\frac{9}{4} \\
l^2=\frac{73}{4} \\
l=\sqrt{\frac{73}{4}} \\
l=\frac{\sqrt{73}}{2}$$

Krok 4. Obliczenie pole powierzchni bocznej stożka.
$$P_{b}=πrl \\
P_{b}=π\cdot4\cdot\frac{\sqrt{73}}{2} \\
P_{b}=2\sqrt{73}π$$

Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy zapiszesz zależność między wysokością stożka i promieniem podstawy np. zaznaczając na rysunku \(3x\) oraz \(8x\) albo zapisując, że \(\frac{H}{r}=\frac{3}{8}\) (patrz: Krok 1.) albo tworząc równanie \(r^2h=24\).
2 pkt
• Gdy stworzysz równanie z jedną niewiadomą np. \(8π=\frac{1}{3}π\cdot(8x)^2\cdot3x\) (patrz: Krok 2.) albo \(r^2\cdot\frac{3}{8}r=24\).
3 pkt
• Gdy obliczysz promień podstawy lub wysokość stożka: \(r=4\) lub \(H=\frac{3}{2}\) (patrz: Krok 2.).
4 pkt
• Gdy otrzymasz oczekiwany wynik.