Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Powinniśmy dostrzec, że łącząc punkt \(S\) z punktami \(A\) oraz \(B\) powstanie nam następujący trójkąt równoramienny \(ABS\):
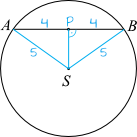
Skąd wiemy, że jest to trójkąt równoramienny? Wynika to z tego, że długości promienia są jednakowe, czyli tym samym ramiona \(AS\) oraz \(BS\) mają tą samą długość. Z własności trójkątów równoramiennych wynika, że ich wysokość dzieli podstawę na dwie równe części, stąd też odcinek \(AB\) o długości \(8cm\) mogliśmy sobie podzielić na dwie części \(AP\) oraz \(PB\), które mają długość równą \(4cm\).
Po dorysowaniu wysokości powstały nam więc dwa trójkąty prostokątne i to właśnie z nich będziemy mogli za chwilę obliczyć poszukiwane długości.
Krok 2. Ocena prawdziwości pierwszego zdania.
Musimy obliczyć długość odległość od punktu \(S\) do odcinka \(AB\), czyli długość odcinka \(SP\). Powinniśmy już dostrzec, że jest to klasyczny trójkąt prostokątny o bokach \(3cm,4cm,5cm\), ale jeśli tego nie widzimy, to korzystając z Twierdzenia Pitagorasa możemy zapisać, że:
$$|SP|^2+4^2=5^2 \\
|SP|^2+16=25 \\
|SP|^2=9 \\
|SP|=3 \quad\lor\quad |SP|=-3$$
Ujemną długość oczywiście odrzucamy, zatem zostaje nam \(|SP|=3cm\), co oznacza, że to zdanie jest prawdą.
Krok 3. Ocena prawdziwości drugiego zdania.
Obwód trójkąta \(ASB\) jest równy:
$$Obw=8cm+5cm+5cm \\
Obw=18cm$$
To zdanie jest więc fałszem.