Czym tak naprawdę są równania, co to znaczy że jakaś liczba spełnia nasze równanie i w jaki sposób rozwiązywać podstawowe przykłady z użyciem tajemniczego „iksa”? Właśnie na te wszystkie pytania odpowiemy sobie w tym temacie.
Do tej pory na matematyce skupialiśmy się głównie na tym, by podać konkretny wynik jakiegoś działania. Ale od czasu do czasu pojawialy się różne zadania, w których trzeba było obliczyć np. jeden składnik sumy, albo też jakiś jeden z czynników mnożenia. Takie działania wyglądały przykładowo tak:
\(□+2=9\) -> co należy wstawić w kratce?
\(8\cdot□=24\) -> jaką liczbę należy pomnożyć przez \(8\), aby otrzymać \(24\)?
Dzisiaj już wiemy, że wszystkie kratki i inne tego typu znaczki możemy zastąpić literami i to z nich od tej pory będziemy korzystać. To co widzisz poniżej, to są właśnie nasze równania.
\(x+2=9\) -> ile wynosi \(x\)? Oczywiście \(7\), bo \(7+2=9\)
\(8x=24\) -> ile wynosi \(x\)? Oczywiście \(3\), bo \(8\cdot3=24\)
No dobrze, ale to były bardzo łatwe przykłady, co z tymi trudniejszymi?
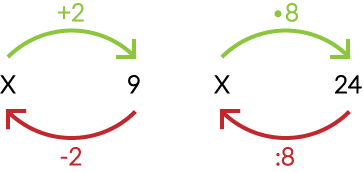
Zanim rozwiążemy sobie trudniejsze przykłady, to poznajmy mechanizm, za pomocą którego jesteśmy w stanie rozwiązać te dwa przykłady powyżej. Tak naprawdę całość moglibyśmy zobrazować w następujący sposób:
Korzystamy w tym momencie z tego, czego uczyliśmy się kilka lat temu:
Dzielenie jest działaniem odwrotnym do mnożenia.
Gdybyśmy chcieli zapisać matematycznie to, co dzieje się na grafie, to otrzymamy:
$$x+2=9 \\
x=9-2 \\
x=7$$
Właśnie rozwiązaliśmy nasze pierwsze równanie!
Podobnie będzie z drugim przykładem:
(wyjątkowo użyjemy kropki mnożenia, tak abyś zobaczył jak to się wszystko odbywa)
$$8\cdot x=24 \\
x=24:8 \\
x=3$$
Teraz jesteśmy już w stanie rozwiązywać podstawowe równania matematyczne z niewiadomą \(x\).
To zadanie wydaje się nieco trudniejsze od poprzednich, bo przed znakiem równości pojawia się więcej działań. Jak rozwiązać takie równanie?
Najpierw obustronnie odejmujemy \(2\), a następnie z uproszczonego równania wyznaczamy bez problemu wartość \(x\). Całość wygląda następująco:
$$7x+2=30\quad|-2 \\
7x=28\quad|:7\\
x=4$$
W takim zadaniu mamy przykład równania, w którym \(x\) występuje po obydwu stronach. Dobrze jest najpierw przenieść wartości \(x\) na jedną stronę (traktując go jak każdą inną liczbę), a następnie należy dokonać obliczeń, które są niemal identyczne jak te z pierwszego przykładu:
$$3x+5=x+9\quad|-x \\
2x+5=9\quad|-5 \\
2x=4\quad|:2\\
x=2$$
Lewa i prawa strona:
W tym dziale będziemy posługiwali się zwrotami: „lewa strona równania” oraz „prawa strona równania”. Wszystko to, co znajduje się przed znakiem równości nazywać będziemy „lewą stroną równania” (skrót: \(L\)), a to co stoi po znaku równości nazwiemy „prawą stroną równania” (skrót: \(P\)).
Aby równanie było prawdziwe to zawsze lewa strona musi się równać prawej, a więc \(L=P\). Liczbę, która jest rozwiązaniem naszego równania nazywamy liczbą spełniającą równanie.
Liczba spełniająca równanie:
Na początku przygody z algebrą spotkasz się także z zadaniami, w których autor poda kilka wariantów liczb, które należy podstawić do równania i sprawdzić, która liczba spełni równanie (czyli po podstawieniu której liczby zajdzie równość \(L=P\)). Rozwiążmy sobie taki prosty przykład, by wiedzieć o co w tym chodzi:
$$3,2x+0,7=7,1$$
Nie pozostaje nam nic innego jak podstawić każdą z tych liczb do naszego równania:
Gdy \(x=1\), wtedy:
$$L=3,2\cdot1+0,7=3,2+0,7=3,9 \\
P=7,1$$
\(L\) nie jest równe \(P\), więc \(x=1\) nie spełnia powyższego równania.
Gdy \(x=2\), wtedy
$$L=3,2\cdot2+0,7=6,4+0,7=7,1 \\
P=7,1$$
\(L=P\), a więc \(x=2\) spełnia nasze równanie.
Gdy \(x=3\), wtedy:
$$L=3,2\cdot3+0,7=9,6+0,7=10,3 \\
P=7,1$$
\(L\) nie jest równe \(P\), więc \(x=3\) nie spełnia powyższego równania.
Ćwiczenia z równaniami:

Ogólnie dobrze wytłumaczone :D
naprawę dobrze wytłumaczone
świetnie wytłumaczone
Fajnie wytłumaczone można się wiele nauczyć
Świetnie wytłumaczone, podczas lekcji nic z tego nie rozumiałam, a zbliżał się sprawdzian. Teraz dzięki temu zdobyłam 5 i naprawdę dziękuję! (Rada dla wszystkich, którzy nadal nie rozumieją dlatego patrzą na komentarze- nie odpuszczajcie za szybko, najlepiej przeczytać to kilka razy, a jeśli naprawdę to nie działa to po prostu zapamiętajcie kolejność rzeczy które mamy robić przy równaniach, chociaż lepsza jest opcja pierwsza).
Bardzo dobrze wytłumaczone
Świetnie wytłumaczone- ten temat był dla mnie czarną magia, ale po przeczytaniu wszystko już rozumiem
Super dziękuje na pewno się przyda
szczerze mówiąc więcej umiem z tej strony niż z lekcji matmy
Super!:)
Tacy nauczyciele powinni uczyć. Jasno i przejrzyście .Dziękuję
Nie było mnie na kilku lekcjach i nie rozumiałam o co chodzi. Dziękuję baaardzo za wytłumaczenie :)
Całkiem dobrze wytłumaczone
dzięki za dobre wytłumaczenie
Mega wytłumaczone :D
super wytłumaczone
super fajnie tłumaczy dostałem 5