Trójkąt równoboczny to trójkąt który ma wszystkie boki równe i wszystkie kąty o jednakowej mierze \(60°\).
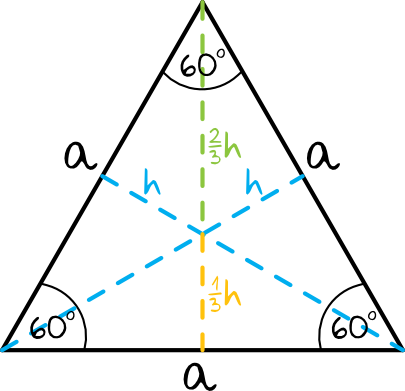
\(a\) – boki trójkąta
\(h\) – wysokość trójkąta
\(\frac{1}{3}h\) – długość od punktu przecięcia się wysokości do boku trójkąta
\(\frac{2}{3}h\) – długość od punktu przecięcia się wysokości do wierzchołka trójkąta
Wzór na pole trójkąta równobocznego:
Pole trójkąta równobocznego możemy oczywiście obliczyć korzystając ze standardowego wzoru \(P=\frac{1}{2}ah\), ale możemy też skorzystać z następującego wzoru:
$$P=\frac{a^2\sqrt{3}}{4}$$
Wzór na wysokość trójkąta równobocznego:
$$h=\frac{a\sqrt{3}}{2}$$
Własności trójkąta równobocznego:
- Każda wysokość jest symetralną i dzieli trójkąt na dwa przystające trójkąty prostokątne.
- Wysokość trójkąta, symetralne boków i dwusieczne kątów pokrywają się ze sobą.
- Wysokości trójkąta równobocznego przecinają się wewnątrz trójkąta w taki sposób, że odcinek od wierzchołka do punktu przecięcia się ma długość \(\frac{2}{3}h\), natomiast odcinek od punktu przecięcia do boku trójkąta ma długość \(\frac{1}{3}h\) (patrz rysunek).
- Punkt przecięcia się wszystkich wysokości jest jednocześnie środkiem okręgu wpisanego i opisanego na trójkącie.
- Promień okręgu wpisanego w trójkąt jest trzykrotnie mniejszy niż wysokość trójkąta.
$$r=\frac{1}{3}h=\frac{a\sqrt{3}}{6}$$ - Promień okręgu opisanego na trójkącie stanowi \(\frac{2}{3}\) wysokości trójkąta i tym samym jest dwa razy większy niż promień okręgu wpisanego.
$$R=\frac{2}{3}h=\frac{a\sqrt{3}}{3}$$
Zobacz także omówienie innych trójkątów: