Rozwiązanie
Wykresem naszej funkcji kwadratowej będzie parabola o ramionach skierowanych do dołu, bo współczynnik kierunkowy \(a\) jest ujemny (mamy minus przed postacią iloczynową). To oznacza, że nasza funkcja będzie mieć mniej więcej taki oto wygląd:
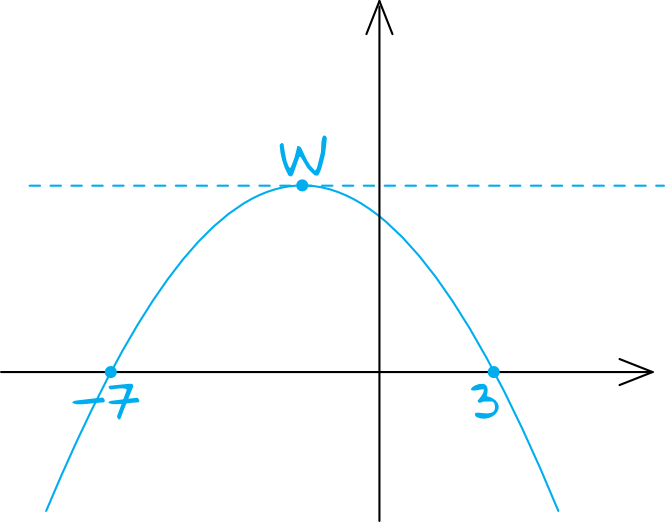
Możemy więc już wywnioskować, że zbiorem wartości będzie przedział od \(-\infty\) aż do wartości w wierzchołku paraboli.
Współrzędne wierzchołka możemy zapisać jako \(W=(p;q)\). Szukamy wartości przyjmowanej w tym wierzchołku, czyli szukamy współrzędnej \(q\) (gdybyśmy szukali odpowiedzi na pytanie dla jakiego argumentu ta wartość jest przyjmowana, to wtedy szukalibyśmy współrzędnej \(p\)). I teraz możemy dojść do tej współrzędnej \(q\) na dwa sposoby:
I sposób - wyznaczając wartość współrzędnej \(p\) i podstawiając ją do wzoru funkcji:
Z postaci iloczynowej możemy odczytać, że miejscami zerowymi naszej funkcji są \(-7\) oraz \(3\). Współrzędna \(p\) wierzchołka paraboli będzie dokładnie pomiędzy tymi dwoma miejscami zerowymi (to wynika z własności wierzchołka), zatem moglibyśmy zapisać, że:
$$p=\frac{-7+3}{2} \\
p=\frac{-4}{2} \\
p=-2$$
Teraz znając wartość \(p=-2\) możemy podstawić \(x=-2\) do wzoru funkcji, dzięki czemu otrzymamy wartość funkcji przyjmowaną w wierzchołku. Zatem:
$$f(-2)=-(-2+7)(-2-3) \\
f(-2)=-(5)(-5) \\
f(-2)=25$$
To oznacza, że wartość przyjmowana w wierzchołku paraboli jest równa \(25\), czyli zbiorem wartości funkcji będzie \((-\infty ;25\rangle\).
II sposób - obliczając wartość \(q\) ze wzoru z tablic:
W tej metodzie skorzystamy ze wzoru:
$$q=\frac{-Δ}{4a}$$
Aby jednak móc skorzystać z tego wzoru musimy najpierw doprowadzić równanie do postaci ogólnej, a następnie musimy policzyć tak zwaną deltę.
Krok 1. Zapisanie równania w postaci ogólnej.
Aby móc obliczyć wartość \(q\) musimy najpierw doprowadzić równanie do postaci ogólnej, zatem:
$$-(x+7)(x-3)=-(x^2-3x+7x-21)= \\
=-(x^2+4x-21)=-x^2-4x+21$$
Krok 2. Obliczenie delty.
Mając postać ogólną możemy już policzyć deltę, która znalazła się w liczniku wzoru na \(q\), zatem:
Współczynniki: \(a=-1,\;b=-4,\;c=21\)
$$Δ=b^2-4ac=(-4)^2-4\cdot(-1)\cdot21=16-(-84)=16+84=100$$
Krok 3. Wyznaczenie wartości współrzędnej \(q\).
Znając deltę możemy zapisać, że:
$$q=\frac{-Δ}{4a} \\
q=\frac{-100}{4\cdot(-1)} \\
q=\frac{-100}{-4} \\
q=25$$
To oznacza, że zbiorem wartości tej funkcji będzie przedział \((-\infty ;25\rangle\).