Rozwiązanie
Krok 1. Obliczenie miejsc zerowych wielomianu.
Aby rozwiązać nierówność musimy najpierw sprawdzić jakie ma miejsca zerowe, czyli musimy sprawdzić dla jakich argumentów \((x+3)^2=0\). Nie musimy wykonywać potęgowania, zastosujemy tutaj własność znaną z funkcji zapisanych w postaci iloczynowej, czyli wartość w nawiasie musimy przyrównać do zera:
$$x+3=0 \\
x=-3$$
Krok 2. Szkicowanie wykresu paraboli.
Zaznaczamy na osi obliczone przed chwilą miejsce zerowe. Ramiona paraboli będą skierowane do góry (bo przed \(x^2\) nie stoi żadna ujemna wartość), zatem całość będzie wyglądać następująco:
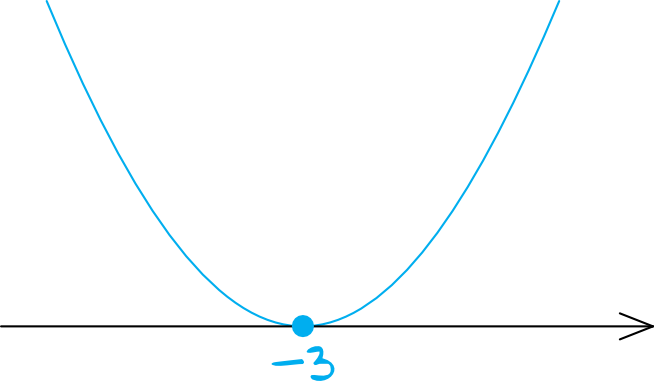
Krok 3. Odczytanie rozwiązania.
Interesują nas wartości mniejsze lub równe zero. Patrząc się na wykres widzimy, że pożądana wartość przyjmowana jest jedynie dla \(x=-3\). Dla wszystkich pozostałych argumentów wartości są większe od zera. To oznacza, że zbiorem rozwiązań nierówności jest tylko liczba \(-3\).