Rozwiązanie
Krok 1. Obliczenie objętości dużego sześcianu.
Wiemy, że nasz duży sześcian składa się z \(64\) małych sześcianików z czego każdy taki mały sześcianik ma krawędź \(1cm\). Objętość każdego takiego małego sześcianu o krawędzi \(1cm\) wynosi:
$$V=1cm\cdot1cm\cdot1cm=1cm^3$$
Jeżeli mamy \(64\) takie sześcianiki, to objętość naszej bryły jest równa:
$$64\cdot1cm^3=64cm^3$$
Krok 2. Obliczenie długości krawędzi sześcianu.
Nam do obliczeń potrzebna będzie długość krawędzi sześcianu, którą wyznaczymy właśnie znając obliczoną przed chwilą objętość bryły:
$$V=a^3 \\
64cm^3=a^3 \\
a=4$$
Krok 3. Obliczenie pola powierzchni sześcianu.
Znając krawędź sześcianu bez problemu obliczymy jego pole powierzchni. Nasz sześcian składa się z sześciu kwadratowych ścian z czego każda ma bok długości \(4cm\), zatem pole powierzchni sześcianu jest równe:
$$P_{p}=6\cdot4cm\cdot4cm \\
P_{p}=6\cdot16cm^2 \\
P_{p}=96cm^2$$
Krok 4. Obliczenie pola powierzchni ścian bocznych nowopowstałej bryły.
Teraz przystąpimy do obliczenia pola powierzchni ścian bocznych nowopowstałej bryły. W tym celu pomoże nam poniższy rysunek:
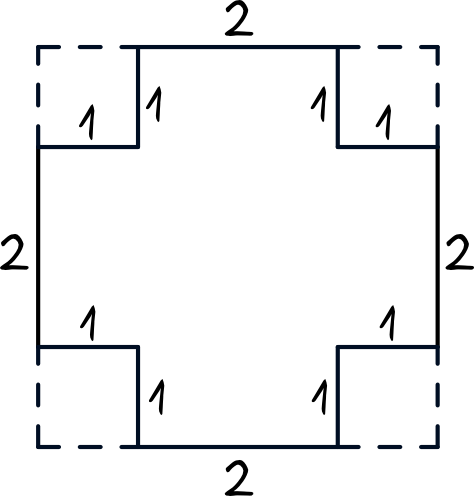
Taka figura znajduje się w każdej ze ścian bocznych, dlatego musimy obliczyć jej pole powierzchni. Możemy to zrobić na różne sposoby np. dzieląc sobie tę figurę na prostokąty i kwadraty, ale najprościej będzie chyba dostrzec, że pole takiej ściany bocznej jest równe polu kwadratu o wymiarach \(4cm\times4cm\) pomniejszonego o cztery małe kwadraty o wymiarach \(1cm\times1cm\):
$$P=(4cm)^2-4\cdot(1cm)^2 \\
P=16cm^2-4cm^2 \\
P=12cm^2$$
Z racji tego iż mamy sześć takich ścian bocznych, to:
$$P_{b}=6\cdot12cm^2 \\
P_{b}=72cm^2$$
Krok 5. Obliczenie pola powierzchni wypustek.

Każda pojedyncza wypustka tworzy nam trzy małe kwadraty o wymiarach \(1cm\times1cm\). Czyli każda taka wypustka powiększa nam pole powierzchni bryły o:
$$3\cdot1cm\cdot1cm=3cm^2$$
Takich wypustek mamy łącznie \(8\), więc ich łączne pole powierzchni będzie równe:
$$8\cdot3cm^2=24cm^2$$
Krok 6. Obliczenie pola powierzchni całkowitej nowopowstałej bryły.
Pole powierzchni nowej bryły jest więc równe:
$$P_{c}=72cm^2+24cm^2 \\
P_{c}=96cm^2$$