Z sześcianu o objętości 27cm^3 usunięto jedną kostkę sześcienną o krawędzi 1cm

Z sześcianu o objętości $27cm^3$ usunięto jedną kostkę sześcienną o krawędzi $1cm$. Ściana usuniętej kostki należała do ściany sześcianu, ale żaden z wierzchołków tej kostki nie należał do krawędzi sześcianu. Pole powierzchni powstałej bryły jest równe:

A. $48cm^2$

B. $54cm^2$

C. $58cm^2$

D. $59cm^2$

Rozwiązanie

Krok 1. Obliczenie wymiarów sześcianu.
Z treści zadania wiemy, że objętość sześcianu jest równa $27cm^3$. Korzystając zatem ze wzoru na objętość tej bryły możemy obliczyć długość krawędzi sześcianu:
$$V=a^3 \\
27cm^3=a^3 \\
a=3cm$$

Krok 2. Sporządzenie rysunku pomocniczego.
Usuwając odpowiedni fragment sześcianu otrzymamy mniej więcej taką oto sytuację:
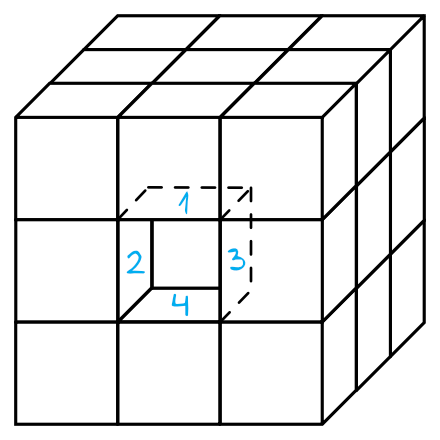
egzamin gimnazjalny

Numerami od $1$ do $4$ zaznaczyłem ściany, które powiększają nam pole powierzchni względem początkowej sytuacji.

Krok 3. Obliczenie pola powierzchni bryły.
Z rysunku wynika, że pole powierzchni tej bryły składać się będzie z sześciu ścian o wymiarach $3cm\times3cm$ oraz czterech wewnętrznych kwadracików, z których każdy ma wymiary $1cm\times1cm$.
W związku z tym:
$$P_{c}=6\cdot3cm\cdot3cm+4\cdot1cm\cdot1cm \\
P_{c}=6\cdot9cm^2+4\cdot1cm^2 \\
P_{c}=54cm^2+4cm^2 \\
P_{c}=58cm^2$$

Odpowiedź

Zadania

Z sześcianu o objętości 27cm^3 usunięto jedną kostkę sześcienną o krawędzi 1cm

Z sześcianu o objętości \(27cm^3\) usunięto jedną kostkę sześcienną o krawędzi \(1cm\). Ściana usuniętej kostki należała do ściany sześcianu, ale żaden z wierzchołków tej kostki nie należał do krawędzi sześcianu. Pole powierzchni powstałej bryły jest równe: