Rozwiązanie
Krok 1. Zapisanie wzoru w postaci kanonicznej.
Współrzędne wierzchołka paraboli związane są z postacią kanoniczną funkcji kwadratowej, czyli postacią \(f(x)=a(x-p)^2+q\), gdzie \(p\) oraz \(q\) to współrzędne wierzchołka paraboli. Skoro więc \(W=(-1,5)\), to możemy zapisać, że:
$$f(x)=a(x-(-1))^2+5 \\
f(x)=a(x+1)^2+5$$
Do pełnego wzoru brakuje nam jeszcze wartości współczynnika \(a\) i właśnie teraz spróbujemy ją wyznaczyć.
Krok 2. Sporządzenie rysunku pomocniczego.
Na podstawie informacji o tym, że w przedziale \(\langle-2,2\rangle\) funkcja osiąga najmniejszą wartość równą \(-4\) musimy wyciągnąć bardzo ważny, choć nieoczywisty wniosek. Wnioskiem do którego powinniśmy dojść jest to, że parabola tej funkcji ma ramiona skierowane do dołu. Skąd to wiemy? W przedziale \(\langle-2,2\rangle\) mieści się nasz wierzchołek, bo przecież \(p=-1\). Gdyby więc ta funkcja miała ramiona skierowane do góry, to ta najmniejsza wartość na pewno byłaby przyjmowana właśnie w wierzchołku, a wiemy że tak nie jest, bo w wierzchołku wartość funkcji jest równa \(5\). Sytuacja z treści zadania wygląda więc następująco:
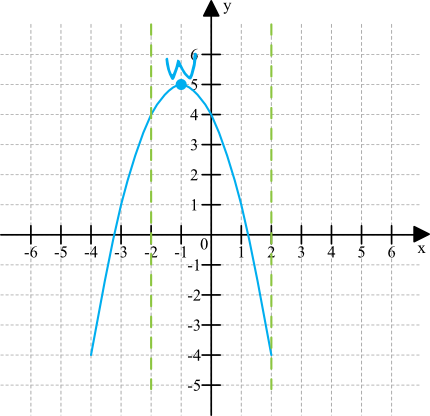
Ale to nie koniec ważnych wniosków. Wartość funkcji w danym przedziale jest najmniejsza (lub największa) na krańcach przedziału lub w wierzchołku. Wierzchołek z tych rozważań już odrzuciliśmy, bo tutaj funkcja przyjmuje największą wartość. To oznacza, że funkcja przyjmuje wartość równą \(-4\) dla jednego z dwóch argumentów: albo dla \(x=-2\), albo dla \(x=2\). Właśnie z rysunku powinniśmy odczytać i wywnioskować, że ta wartość będzie przyjmowana dla argumentu \(x=2\), bo jest to miejsce bardziej oddalone od wierzchołka. To z kolei prowadzi nas do kluczowej informacji, dzięki której będziemy mogli policzyć brakujący współczynnik \(a\) - nasza funkcja przechodzi przez punkt o współrzędnych \(A=(2;-4)\).
Krok 3. Wyznaczenie wartości współczynnika \(a\).
Wiemy już, że wzór funkcji w postaci kanonicznej przybiera postać \(f(x)=a(x+1)^2+5\). Podstawiając do tego wzoru współrzędne punktu \(A=(2;-4)\) obliczymy brakujący współczynnik \(a\):
$$f(x)=a(x+1)^2+5 \\
-4=a\cdot(2+1)^2+5 \\
-4=a\cdot3^2+5 \\
-4=9a+5 \\
9a=-9 \\
a=-1$$
To oznacza, że nasza funkcja w postaci kanonicznej wygląda następująco: \(f(x)=-1(x+1)^2+5\), czyli po prostu \(f(x)=-(x+1)^2+5\)
Krok 4. Przekształcenie wzoru funkcji do postaci ogólnej.
Na sam koniec musimy przekształcić wzór z postaci kierunkowej do postaci ogólnej, a osiągniemy to wykonując potęgowanie, które znalazło się we wzorze:
$$f(x)=-(x+1)^2+5 \\
f(x)=-(x^2+2x+1)+5 \\
f(x)=-x^2-2x-1+5 \\
f(x)=-x^2-2x+4$$