Wyznacz równanie osi symetrii trójkąta o wierzchołkach \(A=(-2,2)\), \(B=(6,-2)\), \(C=(10,6)\).
Zaznaczmy sobie w układzie współrzędnych trzy punkty podane w treści zadania oraz dorysujmy oś symetrii tego trójkąta:
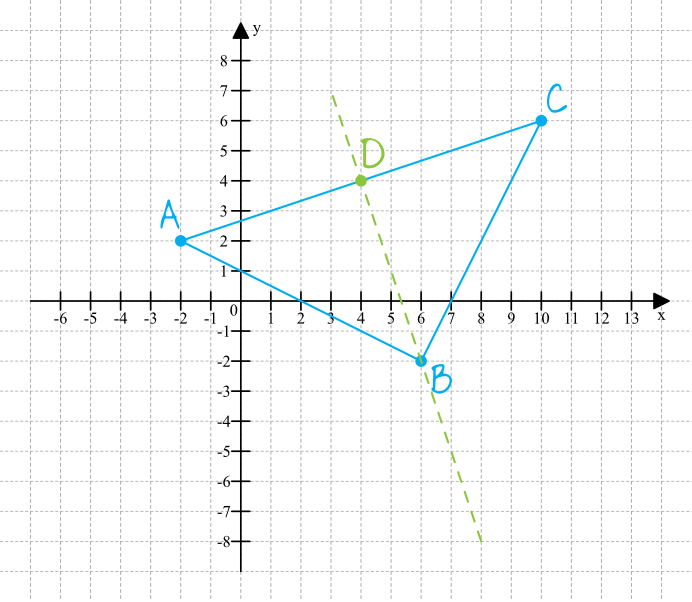
Skąd wiemy, że ta oś symetrii przechodzi przez wierzchołek \(B\)? Skoro trójkąt ma jedną oś symetrii (a tak wynika z treści zadania) to spodziewamy się, że jest to trójkąt równoramienny. Już po rysunku szkicowym widać, że parą ramion równej długości będą ramiona \(AB\) oraz \(BC\), a więc w takim przypadku symetralna będzie przechodzić przez wierzchołek \(B\). Jeśli jednak nie jesteśmy co do tego przekonani, to zawsze możemy sprawdzić długości każdego z boków, używając wzoru na długość odcinka w układzie współrzędnych:
$$|AB|=\sqrt{(x_{B}-x_{A})^2+(y_{B}-x_{A})^2} \\
|AB|=\sqrt{(6-(-2))^2+(-2-2)^2}=\sqrt{64+16}=\sqrt{80} \\
|BC|=\sqrt{(10-6)^2+(6-(-2))^2}=\sqrt{16+64}=\sqrt{80} \\
|AC|=\sqrt{(10-(-2))^2+(6-2)^2}=\sqrt{144+16}=\sqrt{160}$$
Teraz już jesteśmy pewni, że jest to trójkąt równoramienny i że na pewno istnieje tylko jedna oś symetrii, która przechodzi przez punkt \(B\).
Punkt \(D\) jest środkiem odcinka \(AC\), bo wysokość trójkąta równoramiennego dzieli jego podstawę na dwa równe odcinki. Tak więc aby wyznaczyć współrzędne tego punktu \(D\) skorzystamy ze wzorów na środek odcinka:
$$x_{D}=\frac{x_{A}+x_{C}}{2}=\frac{-2+10}{2}=\frac{8}{2}=4 \\
y_{D}=\frac{y_{A}+y_{C}}{2}=\frac{2+6}{2}=\frac{8}{2}=4$$
W związku z tym współrzędnymi naszego punktu są \(D=(4;4)\).
Znajomość współrzędnych punktu \(D\) znacznie ułatwia znalezienie równania osi symetrii, bo wystarczy że skorzystamy ze wzoru na równanie prostej przechodzącej przez dwa punkty. Prostą przechodzącą przez dwa punkty \(B=(6;-2)\) oraz \(D=(4;4)\) możemy opisać następującym równaniem:
$$(y-y_{B})(x_{D}-x_{B})-(y_{D}-y_{B})(x-x_{B})=0 \\
(y-(-2))(4-6)-(4-(-2))(x-6)=0 \\
(y+2)(-2)-6(x-6)=0 \\
-2y-4-6x+36=0 \\
-2y-6x+32=0 \\
-2y=6x-32 \quad\bigg/:(-2)\\
y=-3x+16$$
\(y=-3x+16\)

