Rozwiązanie
Krok 1. Sporządzenie rysunku poglądowego.
Na początku naszkicujmy sobie opisywaną sytuację:
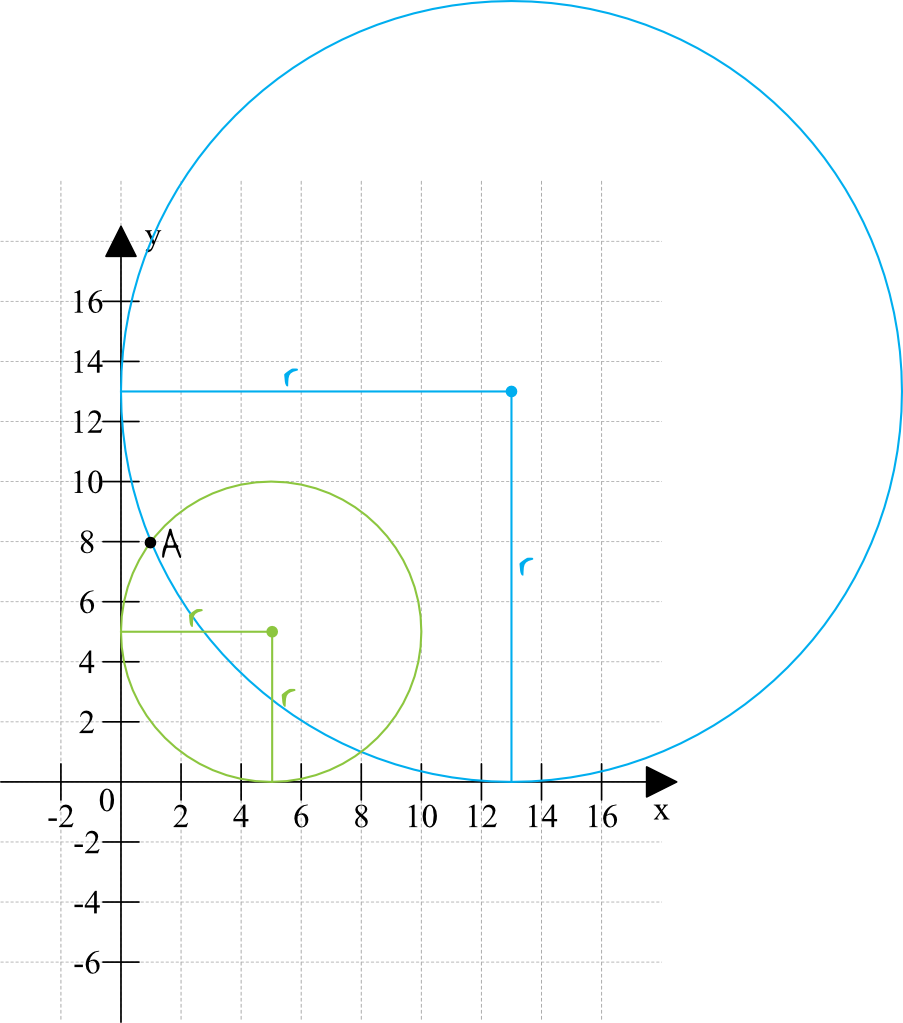
Co z tego rysunku możemy odczytać?
- będą dwa okręgi, które spełnią warunki zadania (aczkolwiek jakbyśmy dostrzegli tylko jeden okrąg, to nic się złego nie stanie, bo wszystko wyjdzie w trakcie obliczeń)
- na pewno te nasze okręgi znajdą się w pierwszej ćwiartce układu współrzędnych
- zarówno w przypadku mniejszego jak i większego okręgu odległości od osi iksów i igreków są równe długości promieni tych okręgów. Skoro tak, to możemy zapisać że współrzędne środka każdego z tych okręgów będą przybierać postać typu \(S=(r;r)\).
Krok 2. Podstawienie współrzędnych punktu \(A=(1;8)\) do wzoru na równanie okręgu.
Z tablic matematycznych możemy odczytać, że wzór na równanie okręgu o środku w punkcie \(S=(a;b)\) oraz promieniu \(r\) ma postać:
$$(x-a)^2+(y-b)^2=r^2$$
Ustaliliśmy już, że środek naszego okręgu ma współrzędne \(S=(r;r)\), czyli możemy całość zapisać jako:
$$(x-r)^2+(y-r)^2=r^2$$
Podstawmy teraz do tego wzoru współrzędne punktu \(A=(1;8)\), czyli \(x=1\) oraz \(y=8\). Otrzymamy w ten sposób:
$$(1-r)^2+(8-r)^2=r^2 \\
1-2r+r^2+64-16r+r^2=r^2 \\
2r^2-18r+65=r^2 \\
r^2-18r+65=0$$
Krok 3. Obliczenie powstałego równania kwadratowego.
Powstało nam równanie kwadratowe, które obliczymy korzystając z delty.
Współczynniki: \(a=1,\;b=-18,\;c=65\)
$$Δ=b^2-4ac=(-18)^2-4\cdot1\cdot65=324-260=64 \\
\sqrt{Δ}=\sqrt{64}=8$$
$$r_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-(-18)-8}{2\cdot1}=\frac{18-8}{2}=\frac{10}{2}=5 \\
r_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-(-18)+8}{2\cdot1}=\frac{18+8}{2}=\frac{26}{2}=13$$
Krok 4. Zapisanie równań okręgów przechodzących przez wskazany punkt.
Z obliczeń wyszły nam dwie możliwości długości promienia: \(r=5 \lor r=13\). Obydwie możliwości są poprawne, żadnej z nich nie odrzucamy (odrzucilibyśmy gdyby np. jedna z nich była ujemna). To oznacza, że warunki naszego zadania spełniają dwa okręgi (czyli tak jak wynikało to z rysunku szkicowego). Musimy już teraz tylko zapisać równania tych okręgów, pamiętając o tym że współrzędne środka okręgów są równe długości promienia:
Okrąg mniejszy: \((x-5)^2+(y-5)^2=5^2\), czyli \((x-5)^2+(y-5)^2=25\)
Okrąg większy: \((x-13)^2+(y-13)^2=13^2\), czyli \((x-13)^2+(y-13)^2=169\)