Rozwiązanie
Krok 1. Zapisanie równania w postaci kanonicznej.
Wzór na równanie okręgu o środku w punkcie \(S=(a;b)\) oraz promieniu \(r\) ma postać:
$$(x-a)^2+(y-b)^2=r^2$$
Spróbujmy przekształcić nasze równanie z treści zadania właśnie do takiej postaci jak powyżej. Możemy to zrobić w następujący sposób:
$$x^2-4x+y^2-2y-4=0 \\
(x-2)^2-4+(y-1)^2-1-4=0 \\
(x-2)^2+(y-1)^2-9=0 \\
(x-2)^2+(y-1)^2=9$$
Krok 2. Odczytanie współrzędnych środka okręgu oraz długości promienia.
Z otrzymanej przed chwilą postaci po przyrównaniu poszczególnych liczb do wzoru na równanie okręgu możemy odczytać, że środek okręgu ma współrzędne \(S=(2;1)\), natomiast promień będzie równy \(r=3\) (bo \(r^2=9)\).
Krok 3. Sporządzenie rysunku pomocniczego i odczytanie rozwiązania.
Na podstawie wyznaczonych informacji stwórzmy prosty rysunek pomocniczy, który pozwoli nam odczytać rozwiązanie zadania.
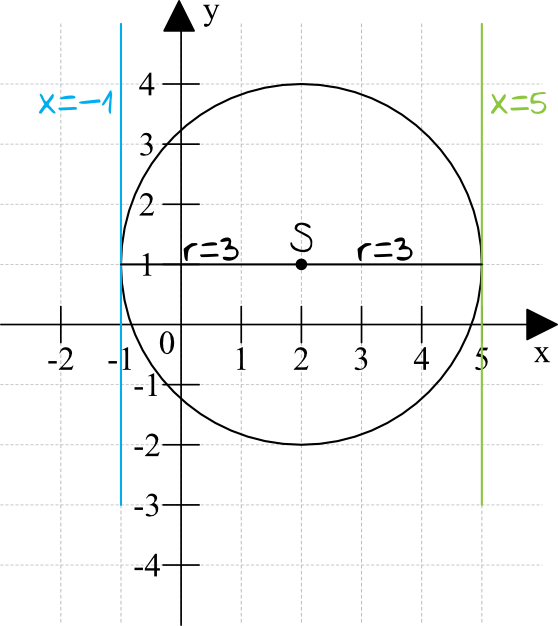
Z rysunku wynika, że proste styczne do okręgu (które są jednocześnie równoległe do osi \(OY\)) to proste \(x=-1\) oraz \(x=5\).