Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Spróbujmy sobie zwizualizować całą sytuację:
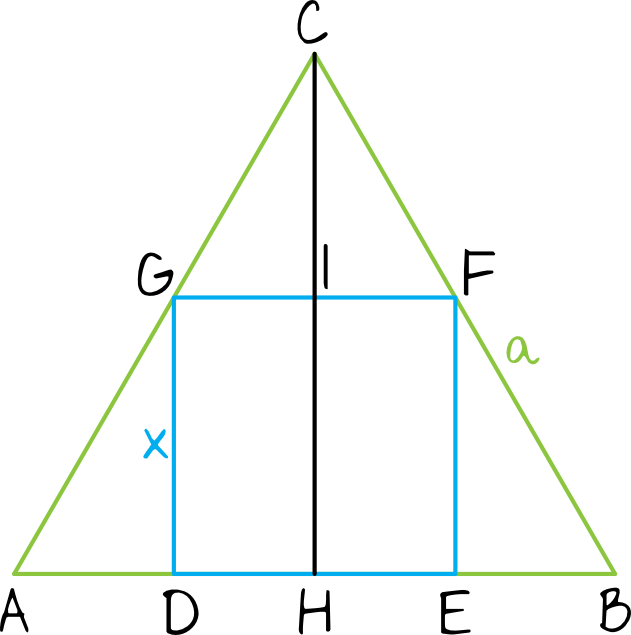
Krok 2. Dostrzeżenie trójkątów podobnych.
Skoro odcinek \(FG\) jest równoległy do podstawy \(AB\), to trójkąt \(GFC\) jest podobny do trójkąta \(ABC\). To z kolei oznacza, że trójkąt \(GFC\) jest także równoboczny.
Krok 3. Zapisanie równania.
Z własności trójkątów równobocznych wiemy, że:
$$|CH|=\frac{a\sqrt{3}}{2}$$
Skoro \(GFC\) jest także trójkątem równobocznym o boku długości \(x\), to:
$$|CI|=\frac{x\sqrt{3}}{2}$$
Patrząc się na rysunek możemy dodatkowo stwierdzić, że:
$$|CI|=|CH|-x$$
Łącząc teraz wyrażenia zapisane przed chwilą otrzymujemy równanie:
$$\frac{x\sqrt{3}}{2}=\frac{a\sqrt{3}}{2}-x$$
Krok 4. Rozwiązanie powstałego równania.
Najlepiej jest całość najpierw wymnożyć przez \(2\), aby pozbyć się ułamków, a następnie przenieść iksy na lewą stronę:
$$\frac{x\sqrt{3}}{2}=\frac{a\sqrt{3}}{2}-x \quad\bigg/\cdot2 \\
x\sqrt{3}=a\sqrt{3}-2x \\
x\sqrt{3}+2x=a\sqrt{3} \\
x(2+\sqrt{3})=a\sqrt{3} \quad\bigg/:(2+\sqrt{3}) \\
x=\frac{a\sqrt{3}}{2+\sqrt{3}} \\
x=\frac{a\sqrt{3}\cdot(2-\sqrt{3})}{(2+\sqrt{3})\cdot(2-\sqrt{3})} \\
x=\frac{2a\sqrt{3}-3a}{4-3} \\
x=\frac{2a\sqrt{3}-3a}{1} \\
x=2a\sqrt{3}-3a \\
x=a(2\sqrt{3}-3)$$