Wysokość trapezu równoramiennego o kącie ostrym \(60°\) i ramieniu długości \(2\sqrt{3}\) jest równa:
\(\sqrt{3}\)
\(3\)
\(2\sqrt{3}\)
\(2\)
Rozwiązanie:
Krok 1. Sporządzenie rysunku poglądowego.
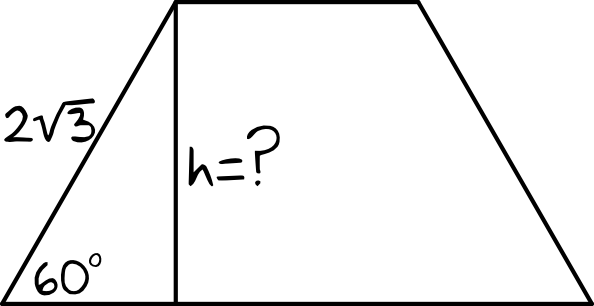
Z rysunku widać wyraźnie, że wartość \(h\) (czyli wysokość naszego trapezu) wyliczymy korzystając z sinusa kąta \(60°\). Możemy też zastosować tutaj własności trójkątów o kątach \(30°, 60°, 90°\).
Krok 2. Obliczenie wysokości trapezu.
$$sin60°=\frac{h}{2\sqrt{3}} \\
\frac{\sqrt{3}}{2}=\frac{h}{2\sqrt{3}} \\
h=\frac{\sqrt{3}}{2}\cdot2\sqrt{3} \\
h=\sqrt{3}\cdot\sqrt{3}=3$$
Odpowiedź:
B. \(3\)

