Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Sytuacja z treści zadania będzie wyglądać mniej więcej w ten oto sposób:
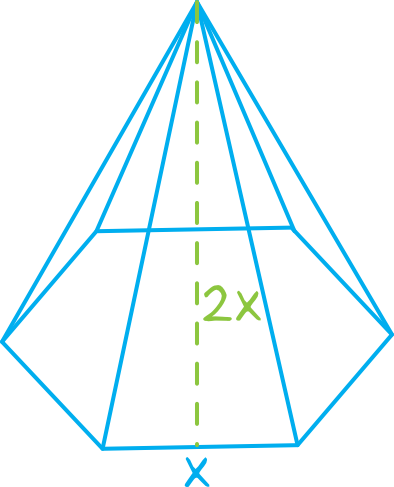
Na podstawie tych danych, musimy teraz obliczyć pole podstawy oraz pole powierzchni bocznej.
Krok 2. Obliczenie pola powierzchni bocznej.
Pole powierzchni bocznej tworzy \(6\) trójkątów o podstawie \(x\) i wysokości \(2x\). Korzystając ze wzoru na pole trójkąta możemy zapisać, że:
$$P_{b}=6\cdot\frac{1}{2}\cdot x\cdot2x \\
P_{b}=6x^2$$
Krok 3. Obliczenie pola podstawy.
Korzystając ze wzoru na pole sześciokąta możemy zapisać, że:
$$P_{p}=6\cdot\frac{x^2\sqrt{3}}{4} \\
P_{p}=\frac{3\sqrt{3}}{2}x^2$$
Krok 4. Obliczenie stosunku pól powierzchni.
Na sam koniec musimy obliczyć stosunek tych dwóch pól, czyli podzielić pole powierzchni bocznej przez pole podstawy:
$$\frac{P_{b}}{P_{p}}=\frac{6x^2}{\frac{3\sqrt{3}}{2}x^2}=\frac{6}{\frac{3\sqrt{3}}{2}}=6:\frac{3\sqrt{3}}{2}=6\cdot\frac{2}{3\sqrt{3}}=\frac{4}{\sqrt{3}}$$
Otrzymany wynik jest poprawny, ale musimy jeszcze wyłączyć niewymierność z mianownika, zatem:
$$\frac{4}{\sqrt{3}}=\frac{4\cdot\sqrt{3}}{\sqrt{3}\cdot\sqrt{3}}=\frac{4\sqrt{3}}{3}$$