Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
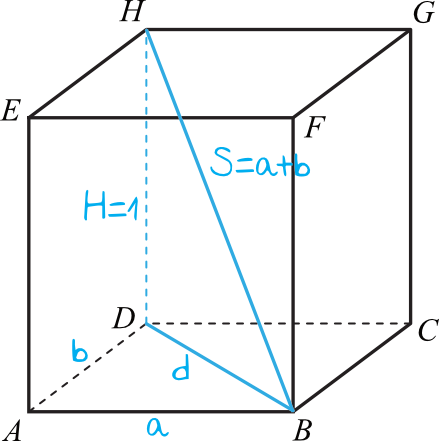
Spróbujmy nanieść na rysunek informacje z treści zadania, które ułatwią nam obliczenia.
Krok 2. Zapisanie długości przekątnej podstawy.
Widzimy, że kluczowym z punktu widzenia zadania będzie trójkąt \(BDH\). W jego dolnej przyprostokątnej znajduje się przekątna podstawy prostopadłościanu, oznaczona symbolem \(d\). Spróbujmy zapisać jej długość za pomocą wyrażeń algebraicznych, korzystając z Twierdzenia Pitagorasa:
$$a^2+b^2=d^2 \\
d=\sqrt{a^2+b^2}$$
Krok 3. Wykorzystanie Twierdzenia Pitagorasa w trójkącie \(BDH\).
Korzystając z Twierdzenia Pitagorasa możemy zapisać, że:
$$d^2+1^2=(a+b)^2 \\
\left(\sqrt{a^2+b^2}\right)^2+1^2=(a+b)^2 \\
a^2+b^2+1=a^2+2ab+b^2 \\
2ab=1 \\
ab=\frac{1}{2}$$
Krok 4. Obliczenie objętości prostopadłościanu.
Spójrzmy na wzór na objętość prostopadłościanu:
$$V=P_{p}\cdot H \\
V=ab\cdot H$$
Znamy wysokość prostopadłościanu, bo \(H=1\). Nie wiemy jaką konkretnie miarę mają odcinki \(a\) oraz \(b\), ale wiemy że ich iloczyn jest równy \(\frac{1}{2}\). I ta wiedza nam w zupełności wystarczy do obliczenia objętości. Podstawiając te dane otrzymamy:
$$V=\frac{1}{2}\cdot1 \\
V=\frac{1}{2}$$