Wykresem funkcji kwadratowej \(f\) jest parabola o wierzchołku \(W=(5,7)\). Wówczas prawdziwa jest równość:
Nie mamy informacji na temat wzoru tej funkcji, ani na temat tego czy ta funkcja kwadratowa ma ramiona skierowane do góry, czy do dołu, ale to akurat nie jest w tym zadaniu dla nas istotne. Załóżmy sobie, że ma ramiona skierowane do dołu, wtedy wykres będzie wyglądał następująco:
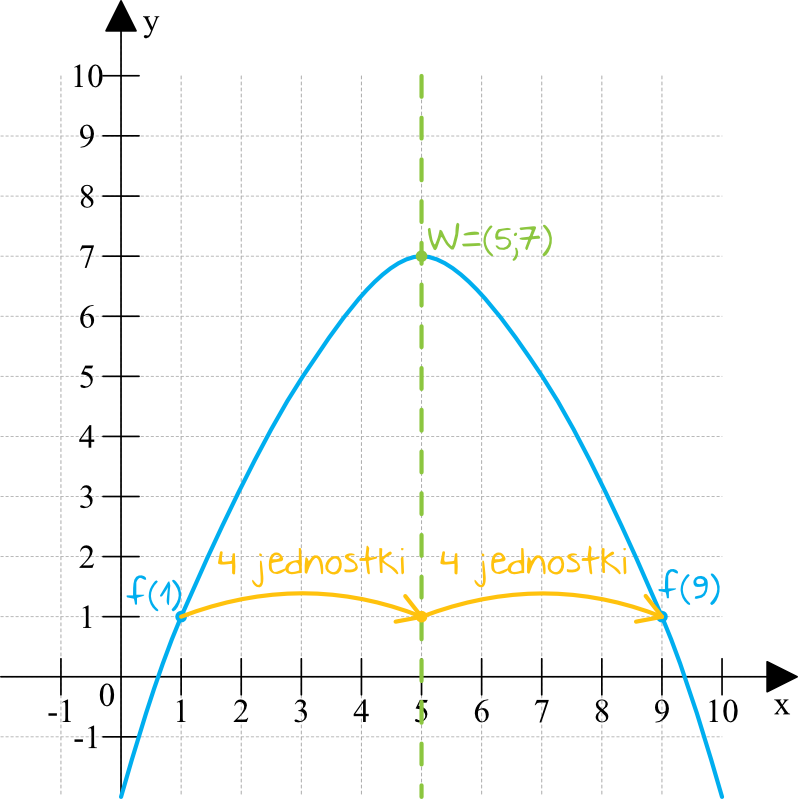
Wykres paraboli jest symetryczny względem prostej przechodzącej dokładnie przez wierzchołek paraboli (patrz rysunek). To oznacza, że wartość równą \(f(1)\) osiągniemy także dla argumentu, którego współrzędna iksowa jest oddalona od wierzchołka o tyle samo jednostek co jest oddalona jedynka. Skoro między jedynką i piątką są \(4\) jednostki, to poszukiwanym argumentem jest \(x=5+4=9\). Zatem \(f(1)=f(9)\).
Podobnie by było, gdyby ramiona były skierowane do góry, dlatego informacja o tym jak dokładnie wygląda ta funkcja nie była nam potrzebna.
A. \(f(1)=f(9)\)

