Rozwiązanie
Aby rozwiązać to zadanie wystarczy narysować parabolę i sprawdzić która prosta przecina ją w dwóch miejscach. Musimy ustalić tylko jak będzie wyglądać ta parabola. Wykres funkcji \(x^2\) umiemy rysować (jest to parabola o wierzchołku w miejscu początku układu współrzędnych). Skoro stoi przed nią minus, to na pewno będzie zwrócona ramionami do dołu. I skoro jeszcze mamy we wzorze \(+1\), to całość będzie przesunięta o jedną kratkę do góry. Całość zatem wyglądać będzie następująco:
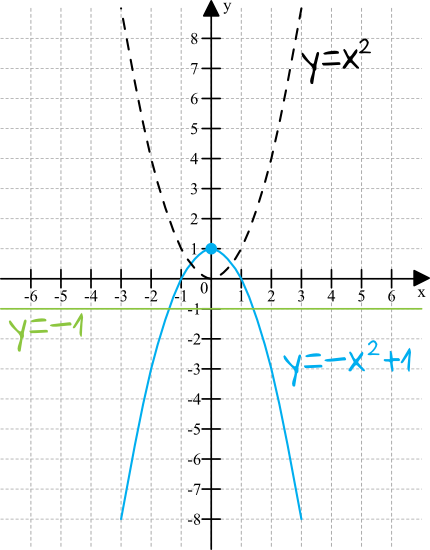
Z rysunku dość jasno wynika, że jedynie prosta \(y=-1\) przecina naszą parabolę w dwóch miejscach.