Rozwiązanie
Krok 1. Wyznaczenie współrzędnych wierzchołka funkcji \(f(x)\).
Funkcję \(f(x)\) mamy zapisaną w postaci kanonicznej \(f(x)=a(x-p)^2+q\) z której bardzo szybko możemy odczytać współrzędne wierzchołka paraboli \(W=(p;q)\). Patrząc się na wzór funkcji możemy stwierdzić, że \(p=-1\) oraz \(q=5\).
Krok 2. Sporządzenie rysunku pomocniczego.
To zadanie będzie najprościej rozwiązać tworząc sobie prosty rysunek pomocniczy na którym zaznaczymy funkcję \(f(x)\) oraz \(g(x)\). O funkcji \(f(x)\) wiemy już, że ma swój wierzchołek w punkcie \(W=(-1;5)\), wiemy też że będzie mieć ramiona skierowane do dołu (bo współczynnik \(a=-1\), czyli jest mniejszy od zera), zatem całość będzie wyglądać następująco:
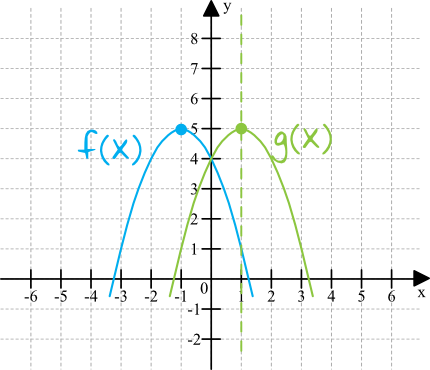
Krok 3. Odczytanie rozwiązania.
Osią symetrii funkcji \(f(x)\) była prosta \(x=-1\) przechodząca przez wierzchołek tej paraboli. Przekształcając tę funkcję względem osi igreków otrzymaliśmy funkcję \(g(x)\), która swój wierzchołek ma w punkcie \(W=(1;5)\), zatem tutaj osią symetrii będzie prosta \(x=1\).