Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Kluczem do sukcesu jest zauważenie, iż podane punkty \(A=(-5,0)\) i \(B=(3,0)\) leżą na osi \(OX\), co prowadzi nas wprost do informacji, że miejscami zerowymi tej funkcji są \(x_{1}=-5\) oraz \(x_{2}=3\). Ogólnie sytuacja z treści zadania będzie wyglądać mniej więcej w ten oto sposób:
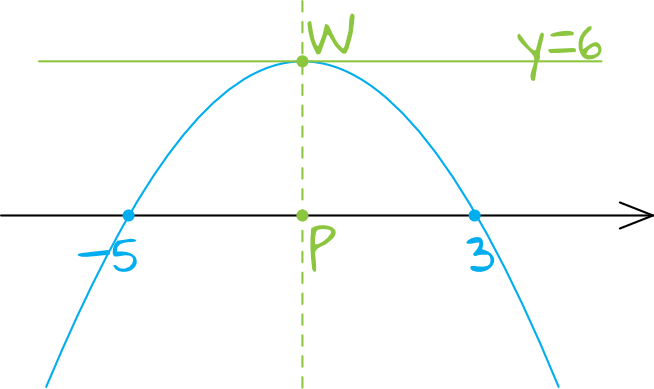
Krok 2. Obliczenie współrzędnej \(p\) wierzchołka paraboli.
Z własności parabol wiemy, że wierzchołek paraboli \(W=(p;q)\) znajduje się dokładnie po środku między miejscami zerowymi. To pozwala nam niemalże błyskawicznie obliczyć współrzędną \(p\) wierzchołka.
$$p=\frac{x_{1}+x_{2}}{2} \\
p=\frac{-5+3}{2} \\
p=\frac{-2}{2} \\
p=-1$$
Krok 3. Wyznaczenie współrzędnej \(q\) wierzchołka paraboli.
W treści zadania mamy informację, że prosta \(y=6\) ma tylko jeden punkt wspólny z naszą parabolą (co zresztą widać na rysunku). To oznacza, że ta prosta musi przechodzić przez wierzchołek (nie ma innej możliwości), co z kolei prowadzi nas do wniosku, że w takim razie współrzędna \(q=6\).
Wiemy już zatem, że \(W=(-1;6)\).
Krok 4. Obliczenie wartości współczynnika \(a\).
Znając współrzędne wierzchołka paraboli, możemy pokusić się o zapisanie wzoru funkcji w postaci kanonicznej:
$$f(x)=a(x-p)^2+q$$
Podstawiając znane współrzędne wierzchołka \(W=(-1;6)\), otrzymamy:
$$f(x)=a(x-(-1))^2+6 \\
f(x)=a(x+1)^2+6$$
Do pełni wzoru brakuje nam znajomości współczynnika \(a\). Aby go poznać, wystarczy podstawić do wyznaczonej postaci współrzędne jednego ze znanych punktów, np. \(A=(-5;0)\). Podstawiając zatem \(x=-5\) oraz \(y=0\), otrzymamy:
$$0=a\cdot(-5+1)^2+6 \\
0=a\cdot(-4)^2+6 \\
0=16a+6 \\
-6=16a \\
a=-\frac{3}{8}$$
To oznacza, że wzorem tej funkcji w postaci kanonicznej jest \(f(x)=-\frac{3}{8}(x+1)^2+6\)
Krok 5. Obliczenie wartości współczynników \(b\) oraz \(c\).
Aby rozwiązać nasze zadanie, musimy poznać wzór funkcji w postaci ogólnej (tylko wtedy poznamy wartości brakujących współczynników \(b\) oraz \(c\)). Póki co, mamy tylko postać kanoniczną, zatem wymnóżmy wszystkie liczby i przekształćmy tym samym zapis do postaci ogólnej:
$$f(x)=-\frac{3}{8}(x+1)^2+6 \\
f(x)=-\frac{3}{8}(x^2+2x+1)+6 \\
f(x)=-\frac{3}{8}x^2-\frac{6}{8}x-\frac{3}{8}+6 \\
f(x)=-\frac{3}{8}x^2-\frac{3}{4}x+5\frac{5}{8}$$
To oznacza, że \(a=-\frac{3}{8}\), \(b=-\frac{3}{4}\) oraz \(c=5\frac{5}{8}\).