Rozwiązanie
Krok 1. Szkicowanie wykresu paraboli.
W treści zadania mamy podaną funkcję w postaci kanonicznej \(f(x)=a(x-p)^2+q\) z której wprost możemy odczytać współrzędne wierzchołka paraboli \(W=(p;q)\). Przyrównując wzór \(f(x)=-\frac{1}{2}(x-3)^2+2\) do postaci kanonicznej widzimy wyraźnie, że \(p=3\) oraz \(q=2\). Dodatkowo też możemy odczytać, że współczynnik \(a=-\frac{1}{2}\), co z kolei będzie oznaczać, że ramiona paraboli będą skierowane do dołu. Nasz wykres będzie więc wyglądał mniej więcej w ten oto sposób:
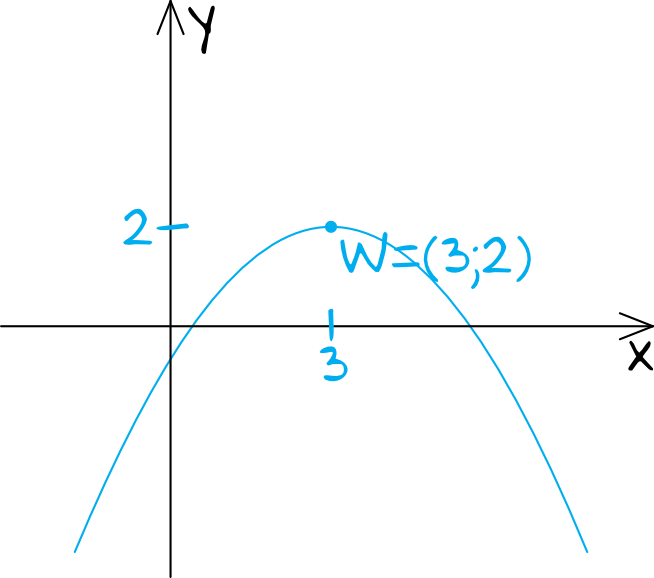
Krok 2. Odczytanie rozwiązania zadania.
Musimy ustalić dla jakiego parametru \(m\) prosta \(y=m\) będzie przecinać naszą parabolę w dwóch miejscach. Po wykresie widzimy wyraźnie, że aby tak się stało, to \(m\) musi być mniejsze od \(2\):
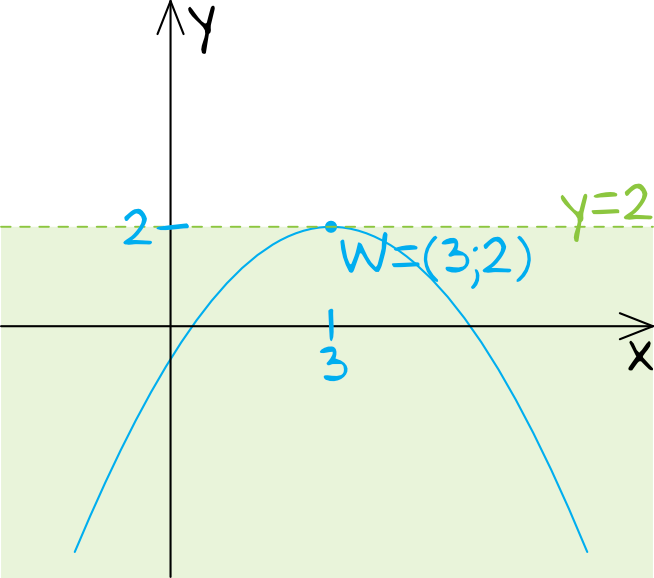
To oznacza, że interesującym nas rozwiązaniem będzie \(m\lt2\).