Wskaż wykres funkcji, która w przedziale \(\langle-4,4\rangle\) ma dokładnie jedno miejsce zerowe.
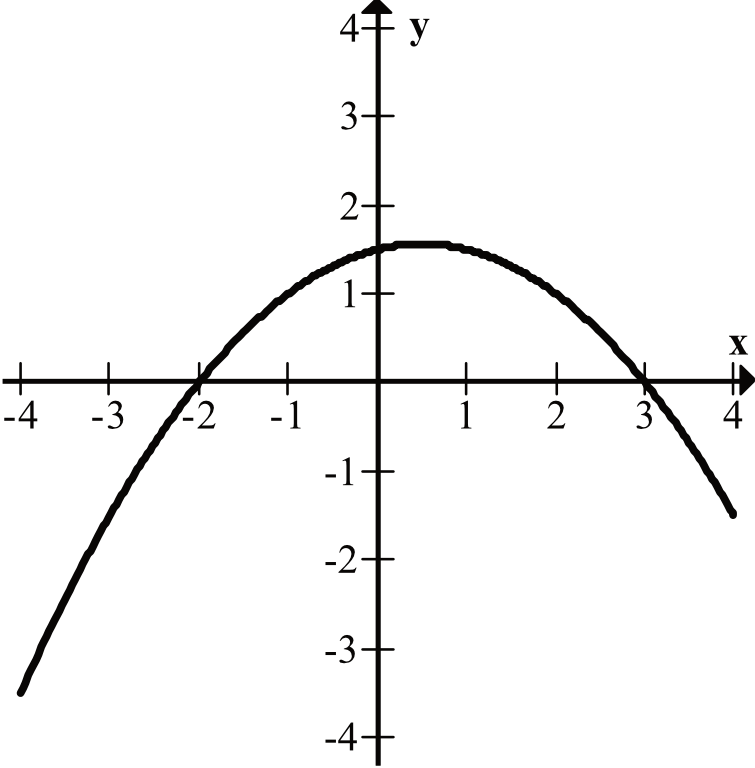
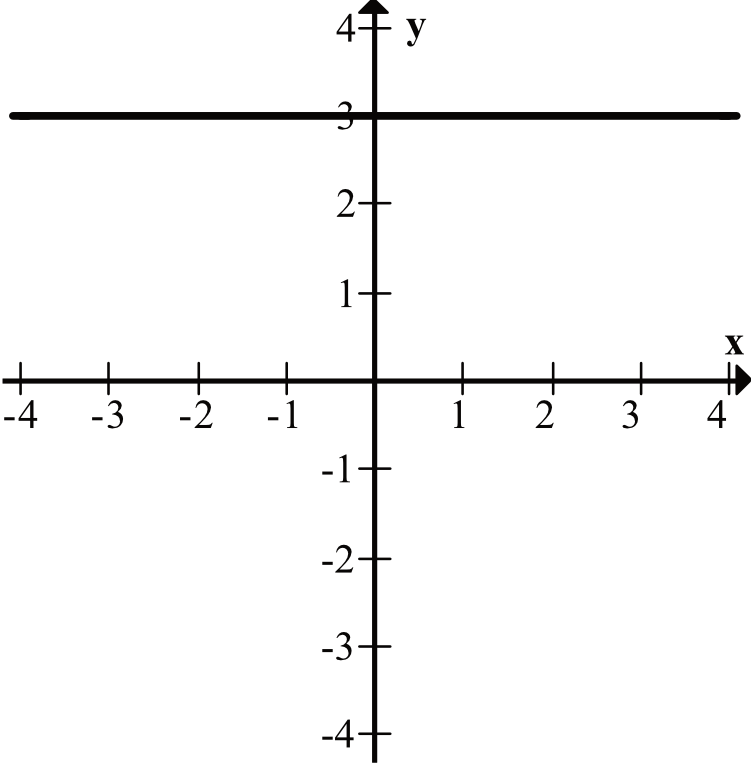
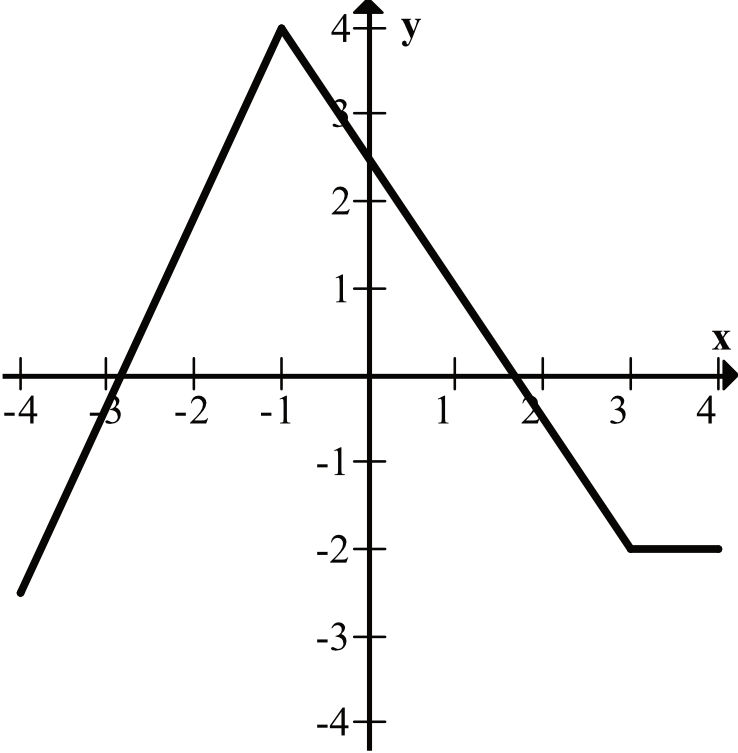
Rozwiązanie:
Miejscem zerowym funkcji jest miejsce przecięcia się wykresu z osią \(Ox\) (czyli jest to taka wartość argumentu \(x\), dla którego funkcja przyjmuje wartość równą zero). Prześledźmy każdy z wykresów:
Pierwsza funkcja ma dwa miejsca zerowe, bo w dwóch miejscach przecina oś \(Ox\).
Druga funkcja nie ma wcale miejsc zerowych.
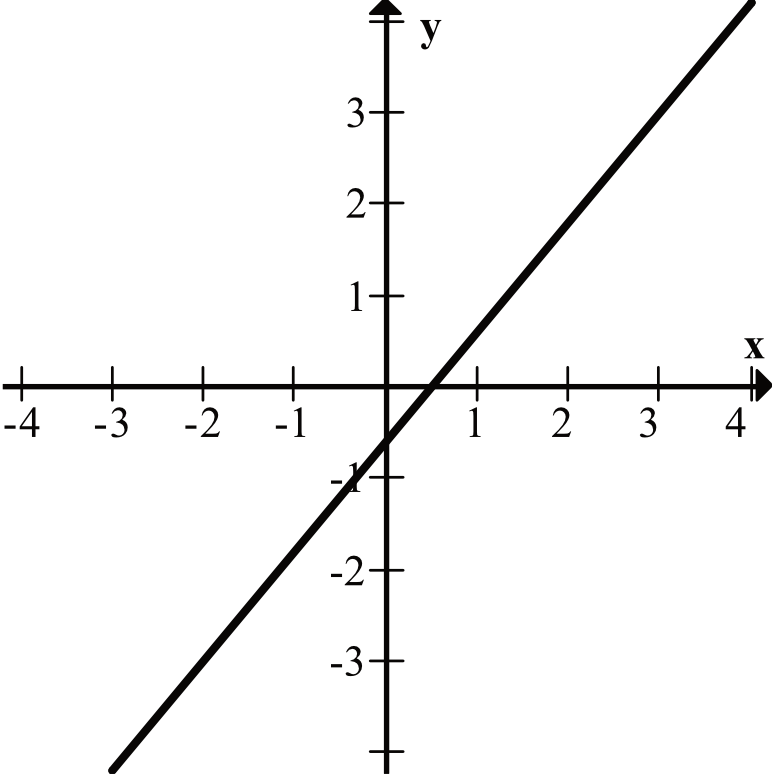
Trzecia funkcja ma dokładnie jedno miejsce zerowe i to jest interesujący nas przypadek.
Czwarta funkcja ma dwa miejsca zerowe, bo w dwóch miejscach przecina oś \(Ox\).
Odpowiedź:


