Wskaż równanie prostej, której fragment przedstawiony jest na poniższym wykresie:
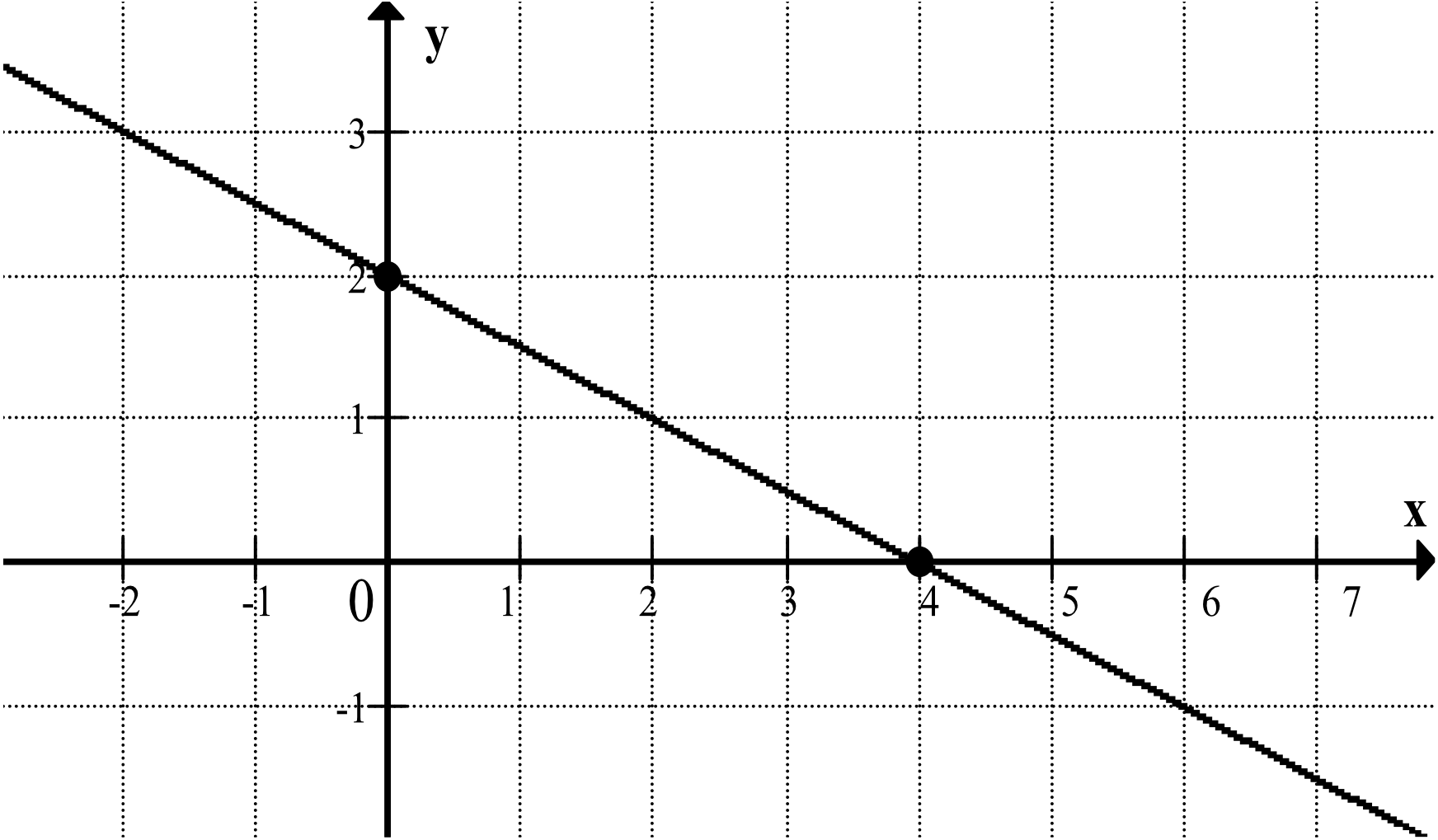
Na podstawie rysunku spróbujmy określić wzór funkcji w postaci ogólnej \(y=ax+b\), którą następnie odpowiednio przekształcimy, tak aby dopasować się do naszych odpowiedzi.
Zaczniemy od współczynnika \(b\), który możemy od razu odczytać z wykresu. Współczynnik \(b\) mówi nam w którym miejscu funkcja liniowa przetnie oś \(Oy\). W naszym przypadku funkcja przecina oś \(Oy\) dla \(y=2\), zatem \(b=2\).
Wiemy już, że nasza funkcja ma postać \(y=ax+2\).
Wykres przecina oś \(Ox\) w punkcie \((4;0)\), czyli dla \(x=4\) funkcja przyjmuje wartość \(y=0\). Podstawmy te współrzędne do wzoru zapisanego w pierwszym kroku i tym samym wyznaczmy wartość współczynnika \(a\):
$$y=ax+2 \\
0=a\cdot4+2 \\
4a=-2 \\
a=-\frac{1}{2}$$
Nasza prosta przyjmuje wzór \(y=-\frac{1}{2}x+2\), jednak nie mamy takiej odpowiedzi w proponowanych. Musimy więc odpowiednio przekształcić to równanie (przenosząc wszystkie wyrazy na jedną stronę), tak aby dopasować się do odpowiedzi:
$$y=-\frac{1}{2}x+2 \\
\frac{1}{2}x+y-2=0 \quad\bigg/\cdot2 \\
x+2y-4=0$$
D. \(x+2y-4=0\)

