Wskaż oś liczbową, na której przedstawiono zbiór wszystkich wartości p, dla których funkcja liniowa f(x)=(8-p^2)x+p

Krok 1. Zapisanie nierówności.
Funkcja liniowa w postaci \(y=ax+b\) jest rosnąca wtedy, gdy współczynnik kierunkowy \(a\) jest większy od zera. W naszym przypadku \(a=8-p^2\), zatem musimy rozwiązać następującą nierówność:
$$8-p^2\gt0$$

Krok 2. Wyznaczenie miejsc zerowych wielomianu.
Powstała nam nierówność kwadratowa, którą precyzyjniej moglibyśmy jeszcze zapisać jako \(-p^2+8\gt0\). Aby rozwiązać taką nierówność, to jak to zwykle bywa, musimy zacząć od wyznaczenia miejsc zerowych, czyli sprawdzenia kiedy \(8-p^2=0\), zatem:
$$-p^2+8=0 \\
p^2=8 \\
p=\sqrt{8} \quad\lor\quad p=-\sqrt{8}$$

Krok 3. Szkicowanie wykresu paraboli.
Zaznaczając na osi liczbowej wartości wyznaczone przed chwilą możemy przystąpić do rysowania paraboli. Jej ramiona będą skierowane do dołu (bo przed \(p^2\) pojawił się minus), zatem całość będzie wyglądać następująco:


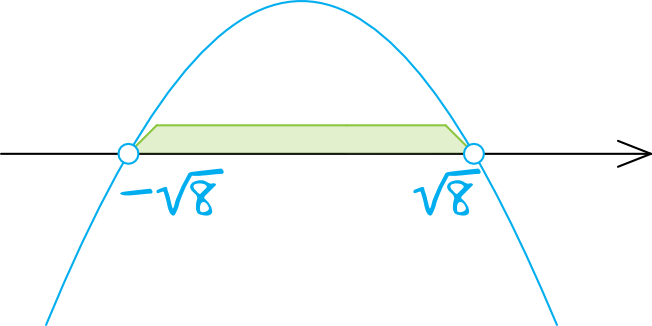
Krok 4. Odczytanie rozwiązania.
Z rysunku wynika, że wartości większe od zera są przyjmowane dla \(p\in(-\sqrt{8};\sqrt{8})\). To z kolei oznacza, że właśnie dla takich wartości naszego \(p\) funkcja liniowa będzie rosnąca. Omawiany przedział został zaprezentowany w trzeciej odpowiedzi.