Wskaż, który zbiór przedstawiony na osi liczbowej jest zbiorem liczb spełniających jednocześnie następujące nierówności: \(3(x-1)(x-5)\le0\) i \(x\gt1\).




Nasza nierówność jest podana w postaci iloczynowej, więc w bardzo łatwy sposób możemy obliczyć jej miejsca zerowe, bo wystarczy przyrównać poszczególne wartości w nawiasach do zera:
$$3(x-1)(x-5)=0 \\
x-1=0 \quad\lor\quad x-5=0 \\
x=1 \quad\lor\quad x=5$$
Ramiona funkcji muszą być skierowane ku górze, bo współczynnik \(a\) stojący przed \(x^2\) po wykonaniu mnożenia wartości w nawiasach byłby na pewno dodatni. Pamiętajmy także o tym, by w tym przypadku punkty \(x=1\) oraz \(x=5\) były z zamalowaną kropką (bo w nierówności mieliśmy znak \(\le\)).
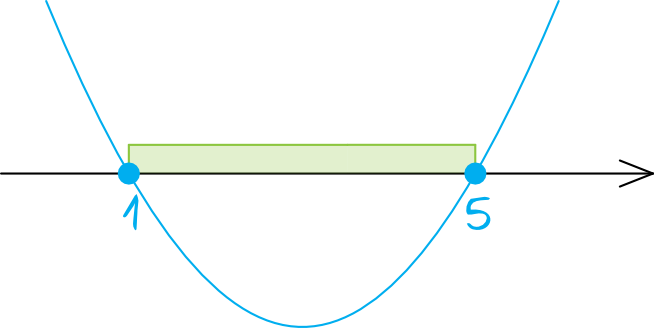
Zgodnie z wykresem nasza funkcja przyjmuje wartości mniejsze lub równe zero dla \(x\in\langle1;5\rangle\).
Wiemy już, że interesującym nas zbiorem liczbowym jest \(x\in\langle1;5\rangle\), ale wbrew pozorom to nie koniec rozwiązywania, bo musimy jeszcze uwzględnić informację z treści zadania, która mówi o tym, że \(x\gt1\). To oznacza, że „jedynka” z naszego zbioru nie spełnia już warunków zadania, tak więc interesującym nas zbiorem będzie \(x\in(1;5\rangle\). To oznacza, że prawidłowy jest wykres z trzeciej odpowiedzi.


