Rozwiązanie
Krok 1. Ocena prawdziwości pierwszego zdania.
Wiemy, że wszystkie klocki są jednakowe. To oznacza, że zdanie jest prawdą, co dobrze pokazuje poniższy rysunek:
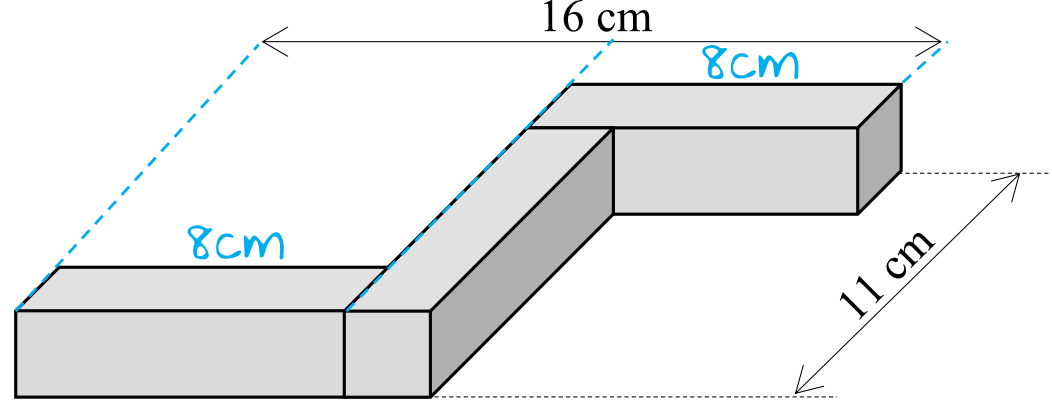
Krok 2. Ocena prawdziwości drugiego zdania.
Do obliczenia objętości potrzebna nam jest znajomość długości krawędzi podstawy, a tę obliczymy tak naprawdę wprost z rysunku:
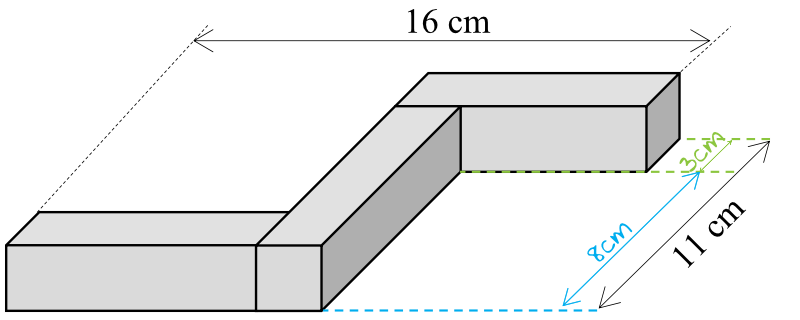
Z treści zadania wiemy, że w podstawie tej bryły jest kwadrat. Wiemy więc, że w podstawie graniastosłupa jest kwadrat o boku \(3cm\), a sam graniastosłup ma wysokość \(8cm\). To oznacza, że objętość tego prostopadłościanu wyniesie:
$$V=P_{p}\cdot H \\
V=3cm\cdot3cm\cdot8cm \\
V=72cm^3$$
Zdanie jest więc prawdą.