Wierzchołek paraboli będącej wykresem funkcji kwadratowej \(y=f(x)\) ma współrzędne \((2,2)\). Wówczas wierzchołek paraboli będącej wykresem funkcji \(g(x)=f(x+2)\) ma współrzędne:
\((4,2)\)
\((0,2)\)
\((2,0)\)
\((2,4)\)
Rozwiązanie:
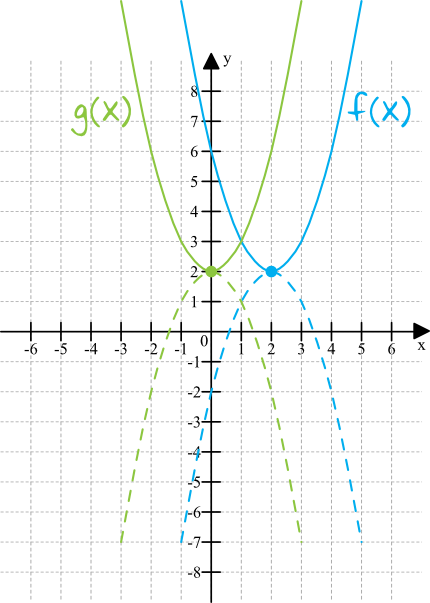
Wykres funkcji \(f(x+2)\) jest przekształcony względem funkcji \(f(x)\) w taki sposób, że parabola będzie przesunięta o \(2\) miejsca w lewo. Nie jest dla nas istotne, czy jest to parabola z ramionami do góry (patrz rysunek: linia ciągła), czy z ramionami do dołu (patrz rysunek: linia przerywana). Jeśli wierzchołek \(f(x)\) był w punkcie \((2;2)\), to wierzchołek \(g(x)\) będzie w punkcie \((0;2)\) w obydwu przypadkach i to jest nasza poszukiwana odpowiedź.
Odpowiedź:
B. \((0,2)\)


Dlaczego przesuwamy w lewo?
Przesunięcia w lewo i prawo nie są tak intuicyjne jak w górę i w dół ;)
Funkcja f(x+2) jest przesunięciem funkcji f(x) o 2 jednostki w lewo.
Funkcja f(x-2) jest przesunięciem funkcji f(x) o 2 jednostki w prawo.