Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Omawiana w treści zadania sytuacja będzie wyglądać mniej więcej w ten oto sposób:
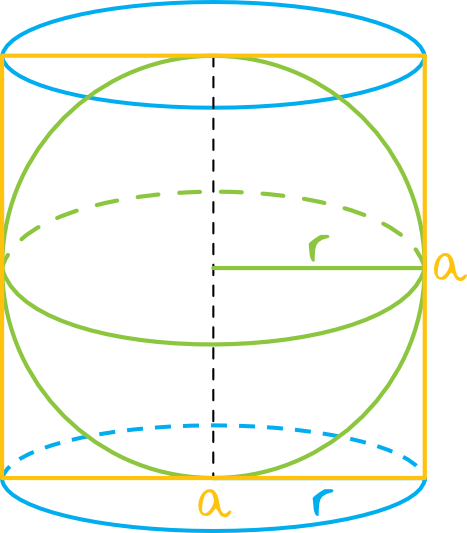
Krok 2. Obliczenie pól powierzchni kuli i walca.
Pola powierzchni kuli i walca obliczymy z następujących wzorów:
$$P_{k}=4\pi r^2 \\
P_{w}=2\pi r(r+h)$$
Z rysunku wynika, że \(r=\frac{1}{2}a\) oraz że \(h=a\). Podstawiając zatem te dane do powyższych wzorów otrzymamy:
$$P_{k}=4\pi\cdot\left(\frac{1}{2}a\right)^2 \\
P_{k}=4\pi\cdot\frac{1}{4}a^2 \\
P_{k}=a^2\pi \\
\text{oraz} \\
P_{w}=2\pi\cdot\frac{1}{2}a\cdot\left(\frac{1}{2}a+a\right) \\
P_{w}=2\pi\cdot\frac{1}{4}a^2+2\pi\frac{1}{2}a^2 \\
P_{w}=\frac{1}{2}a^2\pi+a^2\pi \\
P_{w}=\frac{3}{2}a^2\pi$$
Krok 3. Obliczenie stosunku pól powierzchni kuli i walca.
Naszym zadaniem jest obliczyć stosunek pola powierzchni kuli do pola powierzchni całkowitej walca, zatem:
$$\frac{P_{k}}{P_{w}}=\frac{a^2\pi}{\frac{3}{2}a^2\pi} \\
\frac{P_{k}}{P_{w}}=\frac{1}{\frac{3}{2}} \\
\frac{P_{k}}{P_{w}}=1:\frac{3}{2} \\
\frac{P_{k}}{P_{w}}=1\cdot\frac{2}{3} \\
\frac{P_{k}}{P_{w}}=\frac{2}{3}$$