Rozwiązanie
Krok 1. Obliczenie długości krótszej podstawy trapezu.
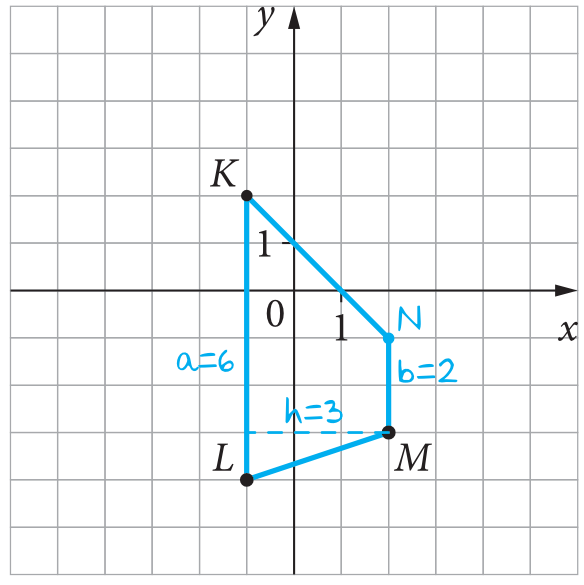
Do obliczenia pola powierzchni trapezu potrzebujemy znać długości obydwu podstaw oraz wysokość figury. Spoglądając na rysunek widzimy, że nasz trapez jest tak jakby przekręcony o \(90°\), ale to nie przeszkadza nam w poznaniu dwóch kluczowych długości. Zwróćmy uwagę, że odcinek \(KL\) ma długość \(6\) jednostek, czyli że \(a=6\). Widzimy też, że jak z punktu \(M\) poprowadzimy prostą prostopadłą, to będzie miała ona długość równą \(3\) jednostki, zatem wysokość \(h=3\).
Skoro \(a=6\) oraz \(h=3\) i wiemy, że \(P=12\), to możemy obliczyć długość drugiej podstawy tego trapezu:
$$P=\frac{1}{2}(a+b)\cdot h \\
12=\frac{1}{2}(6+b)\cdot3 \\
4=\frac{1}{2}(6+b) \\
4=3+\frac{1}{2}b \\
1=\frac{1}{2}b \\
b=2$$
Krok 2. Wyznaczenie współrzędnych wierzchołka \(N\).
Skoro \(b=2\), to wierzchołek \(N\) musi być oddalony o \(2\) jednostki od wierzchołka \(N\). Aby powstał trapez, to ten wierzchołek \(N\) musi być w linii prostej nad \(M\). Skoro więc \(M=(2;-3)\), to \(N=(2;-1)\).