Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Jeżeli punkty \(S\) oraz \(T\) mają nam podzielić odcinek \(AB\) na trzy równe części, to odległość od punkty \(A\) do punktu \(S\) oraz od \(T\) do \(B\) musi być taka sama jak odległość punktu \(S\) od punktu \(T\). Na rysunku będzie to wyglądać w następujący sposób:
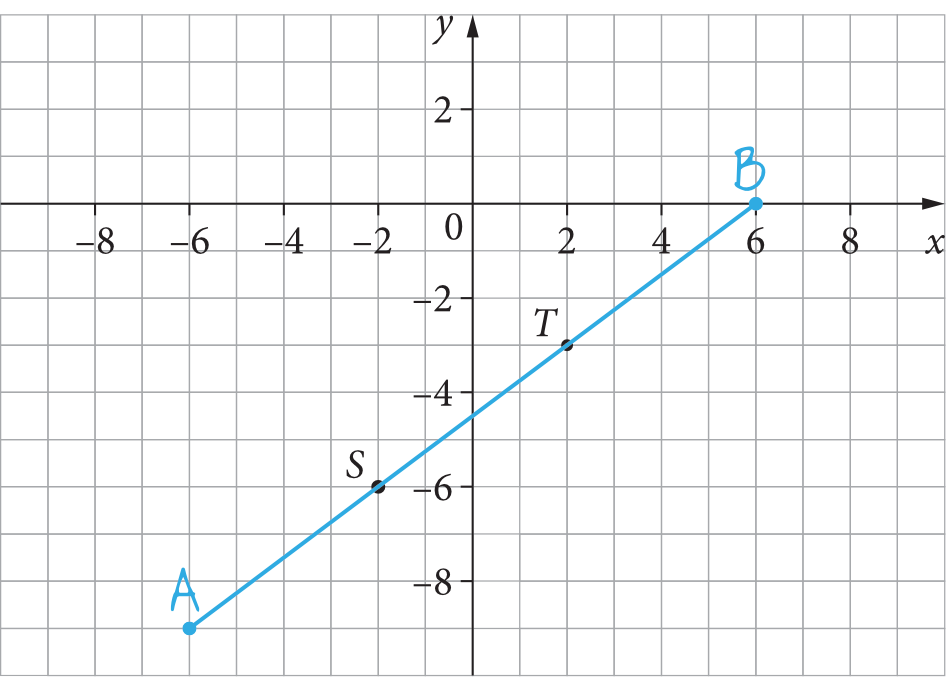
Krok 2. Ocena prawdziwości pierwszego zdania.
Niezależnie od tego jak szczegółowo zrobimy nasz rysunek szkicowy, to powinniśmy zauważyć, że to zdanie jest fałszem. Faktycznie, obie współrzędne punktu \(A\) są ujemne, ale nie można tego powiedzieć o współrzędnych punktu \(B\). Na pewno współrzędna iksowa tego punktu jest dodatnia, a i współrzędna igrekowa nie jest ujemna (będzie ona równa \(0\)).
Krok 3. Ocena prawdziwości drugiego zdania.
Aby poznać długość odcinka \(AB\) musimy skorzystać z Twierdzenia Pitagorasa w układzie współrzędnych. Da się to zrobić w sumie na dwa sposoby. Możemy narysować sobie bardzo duży trójkąt prostokątny w którym odcinek \(AB\) jest przeciwprostokątną, ale jest to dość ryzykowne, bo rysunek szkicowy musi być wtedy naprawdę bardzo dokładny. Wydaje się, ze drugi sposób będzie nieco prostszy, a mianowicie łatwiej będzie nam obliczyć długość odcinka \(ST\), rysując znacznie mniejszy trójkąt prostokątny. Jak poznamy długość odcinka \(ST\) (który jest trzy razy krótszy od odcinka \(AC\)), to bardzo szybko obliczymy długość odcinka \(AB\). Wybierzmy może ten drugi sposób i narysujmy sobie taki oto trójkąt prostokątny:
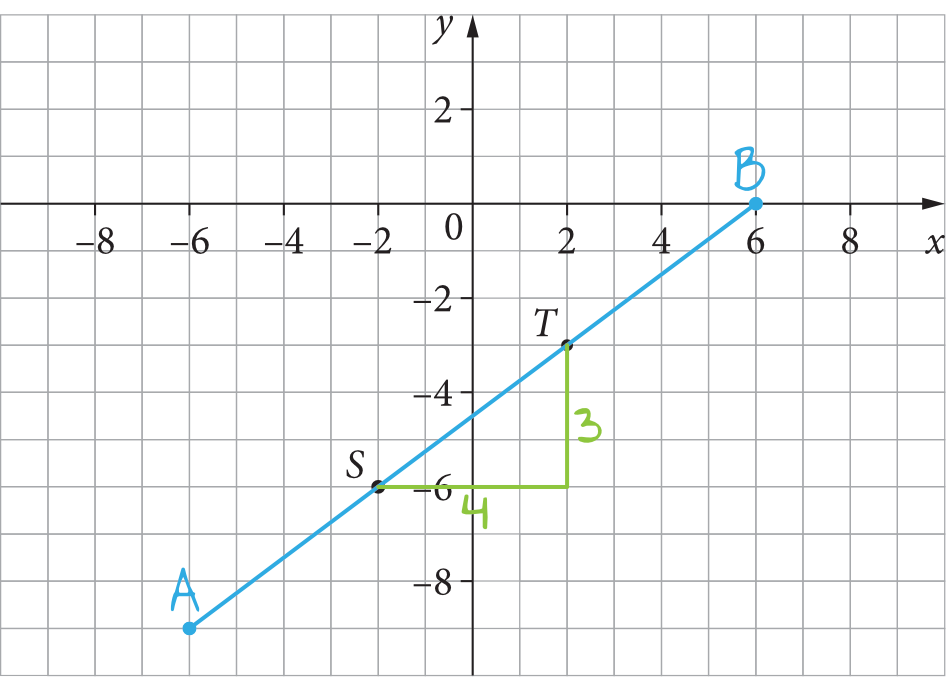
Z rysunku wynika, że odcinek \(ST\) jest przeciwprostokątną trójkąta prostokątnego o przyprostokątnych \(3\) i \(4\), zatem albo z własnego doświadczenia możemy już zapisać, że \(ST=5\), albo też możemy obliczyć to sobie po kolei z Twierdzenia Pitagorasa:
$$3^2+4^2=c^2 \\
9+16=c^2 \\
c^2=25 \\
c=5 \quad\lor\quad c=-5$$
Ujemny wynik nas nie interesuje, zostaje nam zatem \(c=5\), czyli wiemy już, że odcinek \(ST\) ma długość równą \(5\). Nasz odcinek \(AB\) będzie trzy razy dłuższy od odcinka \(ST\), zatem: \(|AB|=3\cdot5=15\). Zdanie jest więc prawdą.