Rozwiązanie
Krok 1. Analiza treści zadania.
Zadanie nie precyzuje który punkt jest środkiem odcinka, a który jest punktem krańcowym odcinka. W związku z tym każdy z trzech punktów \(K, M, P\) może być środkiem naszego odcinka. Musimy więc rozważyć każdy z trzech wariantów
- punkt \(K\) jest środkiem odcinka \(PM\)
- punkt \(M\) jest środkiem odcinka \(PK\)
- punkt \(P\) jest środkiem odcinka \(KM\)
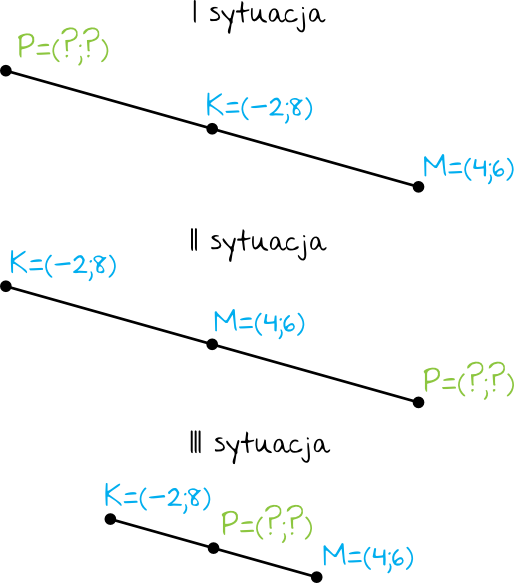
Naszym zadaniem jest więc obliczenie współrzędnych punktu \(P\) w każdym z tych trzech przypadków. Do obliczeń współrzędnych punktu \(P\) skorzystamy ze wzorów na środek odcinka:
$$x_{S}=\frac{x_{A}+x_{B}}{2} \\
y_{S}=\frac{y_{A}+y_{B}}{2}$$
Krok 2. Rozpatrzenie sytuacji w której to punkt \(K\) jest środkiem odcinka.
Skoro \(K=(–2,8)\), to znaczy że:
Współrzędna iksowa punktu \(P\):
$$-2=\frac{x+4}{2} \\
-4=x+4 \\
x=-8$$
Współrzędna igrekowa punktu \(P\):
$$8=\frac{y+6}{2} \\
16=y+6 \\
y=10$$
Zatem \(P=(-8;10)\).
Krok 2. Rozpatrzenie sytuacji w której to punkt \(M\) jest środkiem odcinka.
Współrzędna iksowa punktu \(P\):
$$4=\frac{x-2}{2} \\
8=x-2 \\
x=10$$
Współrzędna igrekowa punktu \(P\):
$$6=\frac{y+8}{2} \\
12=y+8 \\
y=4$$
Zatem \(P=(10;4)\).
Krok 3. Rozpatrzenie sytuacji w której to punkt \(P\) jest środkiem odcinka.
Współrzędna iksowa punktu \(P\):
$$x=\frac{-2+4}{2} \\
x=\frac{2}{2} \\
x=1$$
Współrzędna igrekowa punktu \(P\):
$$y=\frac{8+6}{2} \\
y=\frac{14}{2} \\
y=7$$
Zatem \(P=(1;7)\).