Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Nanosząc na rysunek odpowiednie informacje z treści zadania oraz łącząc środek okręgu z punktem styczności \(S\) otrzymamy następującą sytuację:
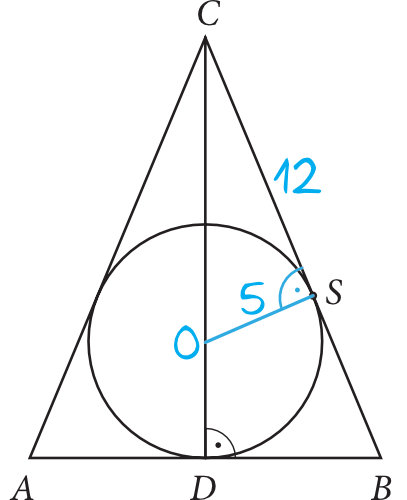
Krok 2. Obliczenie długości odcinka \(CO\).
Spójrzmy na trójkąt prostokątny \(OSC\). Korzystając z Twierdzenia Pitagorasa możemy zapisać, że:
$$|OS|^2+|SC|^2=|CO|^2 \\
5^2+12^2=|CO|^2 \\
25+144=|CO|^2 \\
|CO|^2=169 \\
|CO|=13 \quad\lor\quad |CO|=-13$$
Długość odcinka nie może być ujemna, zatem zostaje nam jedynie \(|CO|=13\).
Krok 3. Obliczenie wysokości \(CD\).
Patrząc się na rysunek możemy teraz zauważyć, że wysokość trójkąta będzie równa sumie długości odcinka \(CO\) (którą obliczyliśmy przed chwilą) oraz \(OD\) (który jest równy długości promienia okręgu), zatem:
$$|CD|=13+5 \\
|CD|=18$$