Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Aby uniknąć działań na ułamkach zapiszmy sobie, że podstawa trójkąta ma długość \(2x\), natomiast wysokość jest równa \(4x\).
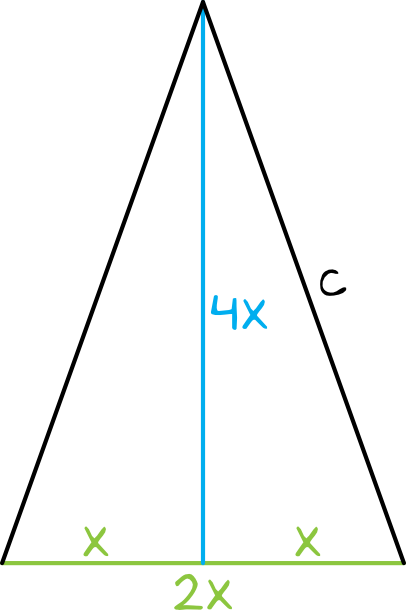
Krok 2. Obliczenie długości przeciwprostokątnej.
Spójrzmy na otrzymany trójkąt prostokątny, bo to z niego teraz będziemy korzystać przy wyznaczeniu wartości sinusa. Do obliczenia sinusa potrzebna nam jest znajomość przeciwprostokątnej trójkąta, a tę wyliczymy z Twierdzenia Pitagorasa. W podstawie trójkąta prostokątnego znajduje się bok długości \(x\) (bo wysokość trójkąta równoramiennego dzieli podstawę na dwie równe części), natomiast druga przyprostokątna ma długość \(4x\). W związku z tym:
$$x^2+(4x)^2=c^2 \\
x^2+16x^2=c^2 \\
17x^2=c^2 \\
c=\sqrt{17}x \quad\lor\quad c=-\sqrt{17}x$$
Wartość ujemną oczywiście odrzucamy, bo długość nie może być ujemna, zatem \(c=\sqrt{17}x\).
Krok 3. Zapisanie wartości sinusa.
Sinus opisuje nam relacje między długością przyprostokątnej leżącej naprzeciwko kąta oraz długością przeciwprostokątej. W związku z tym:
$$sinα=\frac{4x}{\sqrt{17}x} \\
sinα=\frac{4}{\sqrt{17}} \\
sinα=\frac{4\cdot\sqrt{17}}{\sqrt{17}\cdot\sqrt{17}} \\
sinα=\frac{4\sqrt{17}}{17}$$