Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Oznaczmy sobie poszczególne długości na naszym rysunku:
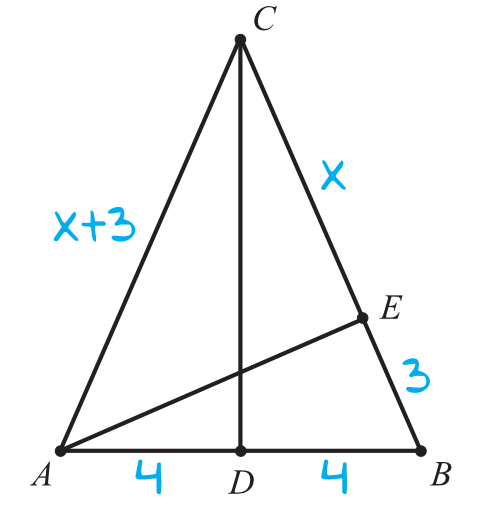
Krok 2. Obliczenie długości odcinka \(AE\).
Korzystając z Twierdzenia Pitagorasa w trójkącie prostokątnym \(ABE\) możemy zapisać, że:
$$|BE|^2+|AE|^2=|AB|^2 \\
3^2+|AE|^2=8^2 \\
9+|AE|^2=64 \\
|AE|^2=55 \\
|AE|=\sqrt{55}$$
Krok 3. Obliczene długości \(x\).
Teraz spójrzmy na trójkąt prostokątny \(AEC\). Korzystając z Twierdzenia Pitagorasa możemy zapisać, że:
$$|AE|^2+|EC|^2=|AC|^2 \\
(\sqrt{55})^2+x^2=(x+3)^2 \\
55+x^2=x^2+6x+9 \\
46=6x \\
x=\frac{46}{6}=\frac{23}{3}$$
Krok 4. Obliczenie długości odcinka \(AC\).
Teraz zgodnie z oznaczeniami na rysunku możemy zapisać, że:
$$|AC|=\frac{23}{3}+3 \\
|AC|=\frac{23}{3}+\frac{9}{3} \\
|AC|=\frac{32}{3}$$