Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Cała sytuacja w układzie współrzędnych będzie wyglądać następująco:
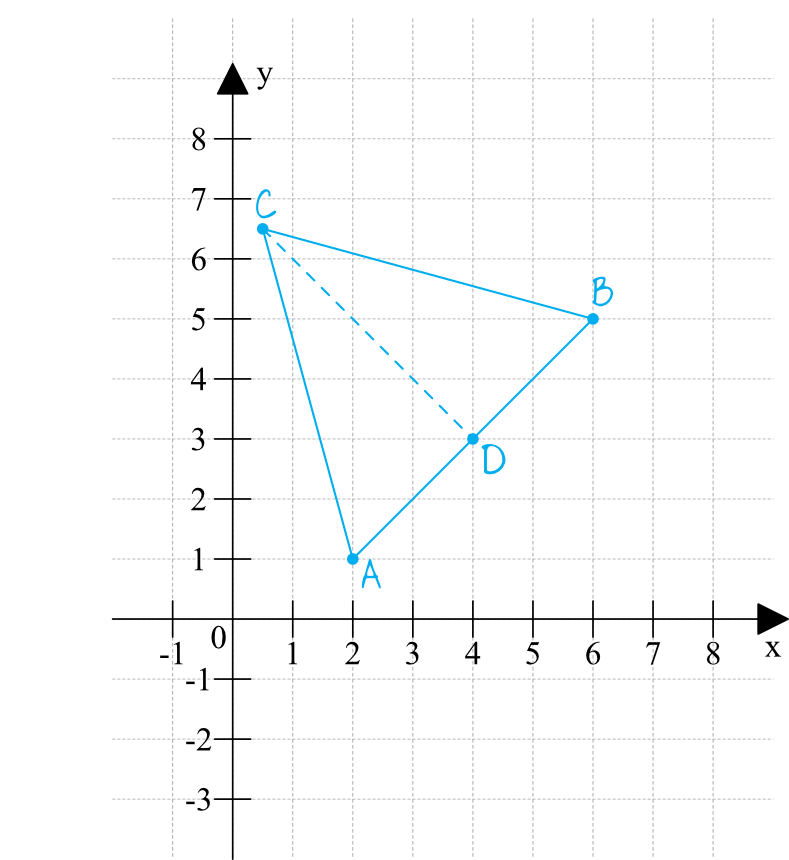
Krok 2. Wyznaczenie współrzędnych punktu \(D\).
Skoro trójkąt jest równoramienny, to wysokość opuszczona na podstawę dzieli ją na dwie równe części. To oznacza, że punkt \(D\) jest środkiem odcinka \(AB\). My znamy współrzędne punktów \(A\) oraz \(B\), zatem korzystając ze wzoru na środek odcinka możemy zapisać, że:
$$D=\left(\frac{x_{A}+x_{B}}{2};\frac{y_{A}+y_{B}}{2}\right) \\
D=\left(\frac{2+6}{2};\frac{1+5}{2}\right) \\
D=\left(\frac{8}{2};\frac{6}{2}\right) \\
D=(4;3)$$
Krok 3. Wyznaczenie współczynnika kierunkowego prostej \(AB\).
Potrzebujemy poznać wartość współczynnika kierunkowego prostej \(AB\), bowiem przyda nam się on do wyznaczenia prostej prostopadłej \(CD\). Znając współrzędne punktów \(A\) oraz \(B\) możemy wyznaczyć nawet cały wzór prostej \(AB\) (korzystając z długiego wzoru z tablic lub z metody układu równań). Mimo wszystko nam wystarczy poznanie jedynie współczynnika kierunkowego prostej \(AB\), a osiągniemy to za pomocą prostego sprytnego wzoru:
$$a=\frac{y_{B}-y_{A}}{x_{B}-x_{A}} \\
a=\frac{5-1}{6-2} \\
a=\frac{4}{4} \\
a=1$$
Krok 4. Wyznaczenie równania prostej \(CD\).
Prosta \(CD\) jest prostopadła do prostej \(AB\). Wiemy, że aby dwie proste były względem siebie prostopadłe, to iloczyn ich współczynników kierunkowych musi być równy \(-1\). Skoro prosta \(AB\) ma ten współczynnik równy \(a=1\), to prosta \(CD\) będzie mieć współczynnik \(a=-1\), bowiem \(-1\cdot1=1\). Skoro tak, to już wiemy, że prosta \(CD\) będzie wyrażać się wzorem \(y=-1x+b\), czyli \(y=-x+b\). Musimy jeszcze tylko wyznaczyć wartość współczynnika \(b\), a zrobimy to podstawiając do tej postaci współrzędne punktu \(D=(4;3)\):
$$y=-x+b \\
3=-4+b \\
b=7$$
Współczynnik \(b\) wyszedł równy \(7\), a to oznacza, że prosta \(CD\) wyraża się wzorem \(y=-x+7\).
Krok 5. Wyznaczenie współrzędnych punktu \(C\).
Z treści zadania wiemy, że \(|CD|=\frac{7\sqrt{2}}{2}\), zatem korzystając ze wzoru na długość odcinka możemy zapisać, że:
$$|CD|=\sqrt{(x_{D}-x_{C})^2+(y_{D}-y_{C})^2} \\
\frac{7\sqrt{2}}{2}=\sqrt{(x_{D}-x_{C})^2+(y_{D}-y_{C})^2} \quad\bigg/^{2} \\
\frac{49}{2}=(x_{D}-x_{C})^2+(y_{D}-y_{C})^2$$
Wiemy, że prosta \(y=-x+7\) przechodzi przez nasz punkt \(C\). To oznacza, że współrzędne punktu \(C\) moglibyśmy zapisać jako \(C=(x;y)\), czyli \(C=(x;-x+7)\). Teraz podstawiając do powyższego wzoru współrzędne \(C=(x;-x+7)\) oraz \(D=(4;3)\) otrzymamy:
$$\frac{49}{2}=(4-x)^2+(3-(-x+7))^2 \\
\frac{49}{2}=(4-x)^2+(3-(-x+7))^2 \\
\frac{49}{2}=(4-x)^2+(3+x-7)^2 \\
\frac{49}{2}=(4-x)^2+(x-4)^2$$
I tu się na chwilę zatrzymamy. Moglibyśmy dostrzec, że prawą stronę równania da się zapisać jako \(2\cdot(x-4)^2\), przez co otrzymalibyśmy:
$$2\cdot(x-4)^2=\frac{49}{2} \\
(x-4)^2=\frac{49}{4}$$
W takiej sytuacji moglibyśmy sprytnie zapisać, że:
$$x-4=\frac{7}{2} \quad\lor\quad x-4=-\frac{7}{2} \\
x=7\frac{1}{2} \quad\lor\quad x=\frac{1}{2}$$
Jednak nie ma co się oszukiwać, z takiego sposobu rozwiązywania rzadko kiedy korzystamy na matematyce, wiele osób nawet go nie kojarzy, no i łatwo tu też o pomyłkę kiedy brakuje nam wprawy. Z tego też względu mając postać \(\frac{49}{2}=(4-x)^2+(x-4)^2\) możemy po prostu wykonać pojawiające się potęgowanie, a rozwiązanie równania obliczymy z użyciem standardowej delty:
$$\frac{49}{2}=(4-x)^2+(x-4)^2 \\
\frac{49}{2}=16-8x+x^2+x^2-8x+16 \\
\frac{49}{2}=2x^2-16x+32 \\
2x^2-16x+7\frac{1}{2}=0 \quad\bigg/\cdot2 \\
4x^2-32x+15=0$$
Współczynniki: \(a=4,\;b=-32,\;c=15\)
$$Δ=b^2-4ac=(-32)^2-4\cdot4\cdot15=1024-240=784 \\
\sqrt{Δ}=\sqrt{784}=28$$
$$x_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-(-32)-28}{2\cdot4}=\frac{32-28}{8}=\frac{4}{8}=\frac{1}{2} \\
x_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-(-32)+28}{2\cdot4}=\frac{32+28}{8}=\frac{60}{8}=7\frac{1}{2}$$
Po dość długich obliczeniach wyszło nam że współrzędna iksowa punktu \(C\) jest równa \(x=\frac{1}{2}\) lub też \(x=7\frac{1}{2}\). Sprawdźmy zatem jakie współrzędne igrekowe otrzymamy dla każdego z tych argumentów:
Gdy \(x=\frac{1}{2}\), to:
$$y=-x+7 \\
y=-\frac{1}{2}+7 \\
y=6\frac{1}{2}$$
Gdy \(x=7\frac{1}{2}\), to:
$$y=-x+7 \\
y=-7\frac{1}{2}+7 \\
y=-\frac{1}{2}$$
Z treści zadania wynika, że obydwie współrzędne punktu \(C\) muszą być dodatnie, zatem ten drugi wariant musimy odrzucić, bo tam wyszło nam \(y=-\frac{1}{2}\). To oznacza, że mamy tylko jedną prawidłową odpowiedź do tego zadania i będzie to \(C=\left(\frac{1}{2};6\frac{1}{2}\right)\).