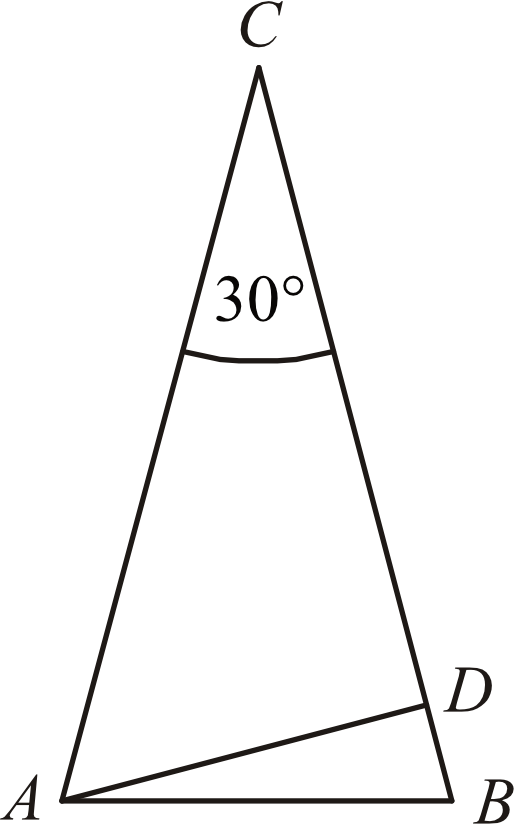
W trójkącie równoramiennym \(ABC\) dane są \(|AC|=|BC|=6\) i \(|\sphericalangle ACB|=30°\) (zobacz rysunek). Oblicz wysokość \(AD\) trójkąta opuszczoną z wierzchołka \(A\) na bok \(BC\).
Rozwiązanie:
Musimy zauważyć, że trójkąt \(ADC\) jest trójkątem prostokątnym (bo wysokość zawsze jest opuszczana pod kątem prostym). To dość ważna informacja, bo dzięki niej wiemy, że możemy skorzystać z funkcji trygonometrycznych. Skoro znamy miarę kąta jednego z kątów ostrych i znamy długość przeciwprostokątnej \(AC\), to możemy skorzystać z funkcji sinusa:
$$sin30°=\frac{|AD|}{|AC|} \\
\frac{1}{2}=\frac{|AD|}{6} \\
|AD|=3$$
Odpowiedź:
\(|AD|=3\)

