Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Skoro mamy trójkąt prostokątny, w którym jeden z kątów ostrych ma \(30°\), to wiemy już, że mówimy o charakterystycznym trójkącie o kątach \(30°, 60°, 90°\). Krótsza przyprostokątna to ta, która leży naprzeciwko kąta o mierze \(30°\) (oznaczamy ją zwyczajowo jako \(a\)). Sytuacja z treści zadania będzie więc wyglądać następująco:
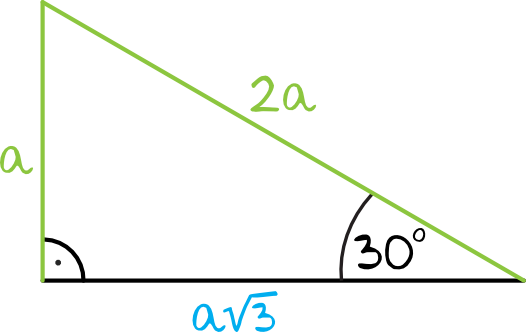
Krok 2. Obliczenie długości dłuższej przyprostokątnej.
Z treści zadania wynika, że suma długości krótszej przyprostokątnej i przeciwprostokątnej jest równa \(12 cm\). Zgodnie z oznaczeniami na rysunku możemy więc zapisać, że:
$$a+2a=12cm \\
3a=12cm \\
a=4cm$$
Dłuższa przyprostokątna ma długość \(a\sqrt{3}\), zatem będzie miała ona miarę:
$$b=4\sqrt{3}cm$$