W trójkącie prostokątnym o długościach przyprostokątnych \(2\) i \(5\) cosinus większego z kątów ostrych jest równy:
\(\frac{5}{2}\)
\(\frac{2}{5}\)
\(\frac{2}{\sqrt{29}}\)
\(\frac{5}{\sqrt{29}}\)
Rozwiązanie:
Krok 1. Sporządzenie rysunku poglądowego.
Narysujmy sobie ten trójkąt by przede wszystkim dostrzec w którym miejscu znajdzie się większy z kątów ostrych:
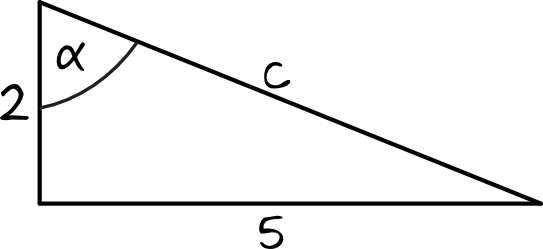
Cosinus zaznaczonego kąta będzie więc stosunkiem długości przyprostokątnej przy tym kącie do długości przeciwprostokątnej.
$$cosα=\frac{2}{c}$$
Krok 2. Obliczenie długości przeciwprostokątnej.
Korzystając z Twierdzenia Pitagorasa:
$$2^2+5^2=c^2 \\
4+25=c^2 \\
c^2=29 \\
c=\sqrt{29}$$
Krok 3. Obliczenie wartości cosinusa.
Możemy teraz wrócić do obliczenia wartości cosinusa, a tak naprawdę wystarczy już tylko podstawić obliczoną przed chwilą długość przeciwprostokątnej:
$$cosα=\frac{2}{\sqrt{29}}$$
Odpowiedź:
C. \(\frac{2}{\sqrt{29}}\)


dziękuje