Rozwiązanie
Krok 1. Obliczenie długości boku drugiej przyprostokątnej.
Korzystając z Twierdzenia Pitagorasa możemy obliczyć długość drugiej przyprostokątnej tego trójkąta:
$$5^2+b^2=13^2 \\
25+b^2=169 \\
b^2=144 \\
b=12 \quad\lor\quad b=-12$$
Krok 2. Sporządzenie rysunku pomocniczego.
Sytuacja z treści zadania (w tym kąt ostry, który nas najbardziej interesuje) będzie wyglądać następująco:
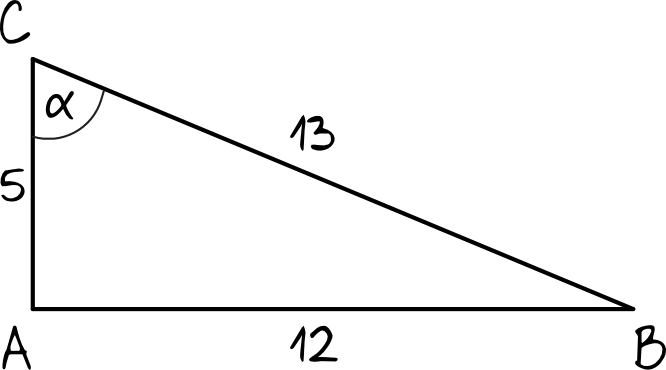
Przy okazji warto pamiętać, że w trójkącie prostokątnym zawsze będzie tak, że większy kąt ostry znajduje się przy krótszym boku.
Krok 3. Obliczenie sinusa kąta ostrego.
Sinus to stosunek długości przyprostokątnej naprzeciwko kąta względem długości przeciwprostokątnej, zatem:
$$sinα=\frac{12}{13}$$