Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Boki trójkąta są tak naprawdę stycznymi do okręgu, zatem wykorzystując własności stycznych do okręgu możemy stworzyć taki oto rysunek pomocniczy:
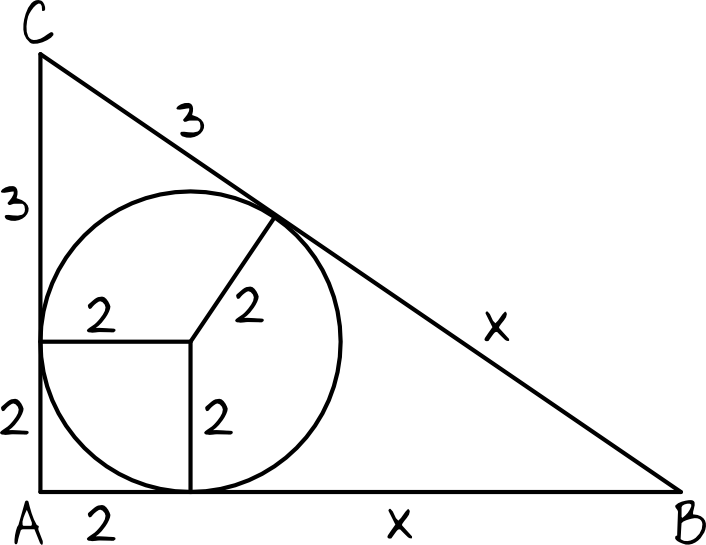
Krok 2. Obliczenie wartości niewiadomej \(x\).
Skoro jest to trójkąt prostokątny, to możemy skorzystać z Twierdzenia Pitagorasa:
$$|AB|^2+|AC|^2=|BC|^2 \\
(2+x)^2+5^2=(3+x)^2 \\
4+4x+x^2+25=9+6x+x^2 \quad\bigg/-x^2 \\
4+4x+25=9+6x \\
4x+29=9+6x \\
-2x+29=9 \\
-2x=-20 \\
x=10$$
Krok 3. Obliczenie długości boku \(AB\).
Skoro \(x=10\), to znaczy że:
$$|AB|=2+x \\
|AB|=2+10 \\
|AB|=12$$
Krok 4. Obliczenie pola powierzchni trójkąta.
Wiemy już, że podstawa trójkąta ma długość \(12\) i wysokość \(5\), zatem:
$$P=\frac{1}{2}ah \\
P=\frac{1}{2}\cdot12\cdot5 \\
P=6\cdot5 \\
P=30$$