Rozwiązanie
Zadanie jest dość trudne, bo nie mamy zbyt wiele informacji na temat trójkąta \(ABC\). Gdyby bok trójkąta przechodził przez punkt \(S\), to mielibyśmy trójkąt prostokątny, ale niestety tutaj tak nie jest. Całość zadania opiera się jednak nie na trójkącie, a na kątach wpisanych i środkowych. Spójrzmy na kąt \(ABC\) o mierze \(40°\). Jest to kąt opisany na łuku \(AC\). To oznacza, że jak dorysujemy prostą \(AS\), to powstanie nam kąt środkowy \(ASC\) (który także jest opisany na łuku \(AC\)), który będzie miał miarę dwukrotnie większą, czyli:
$$|\sphericalangle ASC|=2\cdot40° \\
|\sphericalangle ASC|=80°$$
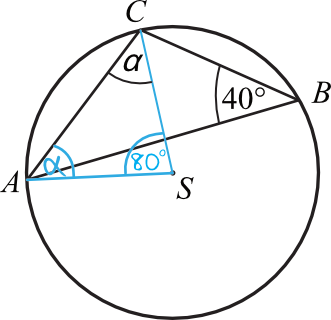
Teraz spójrzmy na powstały trójkąt \(ASC\). Jest to trójkąt równoramienny (ramiona \(AS\) oraz \(CS\) mają długość promienia okręgu). To z kolei oznacza, że kąty przy podstawie \(AC\) muszą mieć jednakową miarę. Skoro więc kąt \(ASC\) ma miarę \(100°\), to:
$$α=(180°-80°):2=100°:2=50°$$