Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Zwróćmy uwagę, że podany trójkąt jest równoramienny (bo ramiona \(AC\) oraz \(BC\) są jednakowej długości). Skoro tak, to wysokość \(CD\) podzieli nam trójkąt na dwa identyczne trójkąty prostokątne (wysokość trójkąta równoramiennego zawsze dzieli podstawę na dwie równe części). Oznaczmy więc podstawę trójkąta jako \(x\), a ramiona jako \(y\), otrzymując taką oto sytuację:
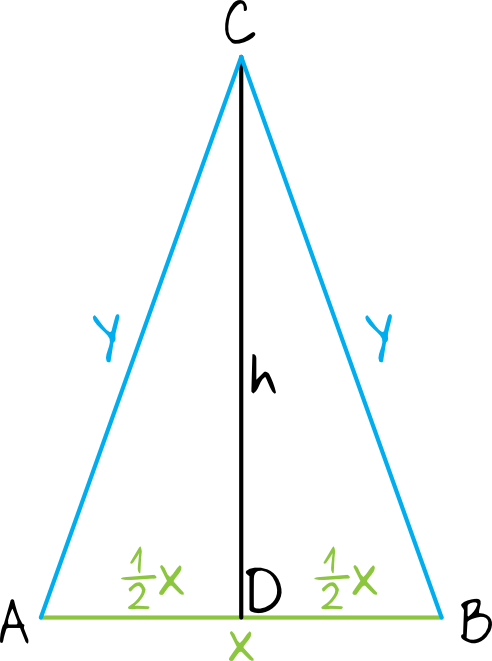
Krok 2. Ocena prawdziwości pierwszego zdania.
Pierwsze zdanie jest na pewno fałszem. Trójkąt \(BCD\) musi mieć taki sam obwód jak trójkąt \(ACD\), gdyż są to trójkąty przystające, zatem obwód trójkąta \(BCD\) jest równy \(24cm\).
Krok 3. Ocena prawdziwości drugiego zdania.
Spójrzmy na trójkąt \(ACD\). Podstawa ma długość \(\frac{1}{2}x\), druga przyprostokątna ma długość \(h\), a przeciwprostokątna to \(y\). Czyli:
$$\frac{1}{2}x+y+h=24$$
Teraz spójrzmy na trójkąt \(ABC\). Tutaj obwód jest równy \(36 cm\), czyli zgodnie z oznaczeniami na rysunku:
$$x+2y=36$$
Jeżeli podzielimy obydwie strony tego równania przez \(2\), to otrzymamy:
$$\frac{1}{2}x+y=18$$
Podstawiając teraz równanie \(\frac{1}{2}x+y=18\) do obwodu trójkąta \(ACD\), otrzymamy:
$$18+h=24 \\
h=6$$
Zdanie jest więc prawdą.