Rozwiązanie
Krok 1. Obliczenie miary kąta \(ASD\).
Aby lepiej opisać to zadanie, przyjmijmy, że miejsce przecięcia się wysokości to punkt \(S\).
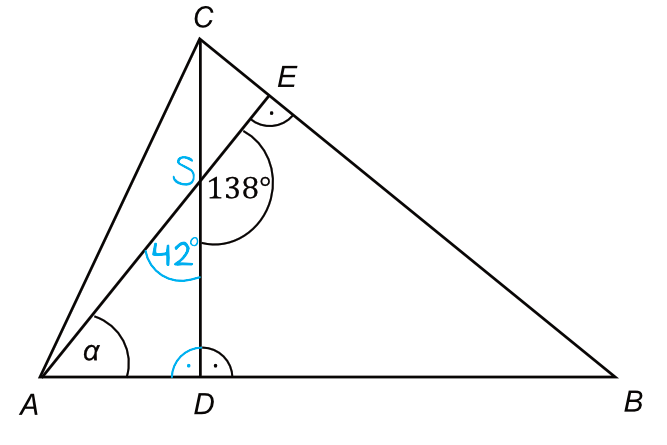
Zwróćmy teraz uwagę, że kąt \(ESD\) oraz \(ASD\) to kąty przyległe, czyli takie, których łączna miara jest równa \(180°\). Skoro tak, to kąt \(ASD\) ma miarę:
$$|\sphericalangle ASD|=180°-138°=42°$$
Krok 2. Obliczenie miary kąta \(\alpha\).
Spójrzmy teraz na trójkąt prostokątny \(ADS\). Skoro kąt \(ASD\) ma miarę \(42°\), to:
$$\alpha=180°-90°-42°=48°$$