Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Skoro trapez jest równoramienny, to sytuacja z treści zadania będzie wyglądać następująco:
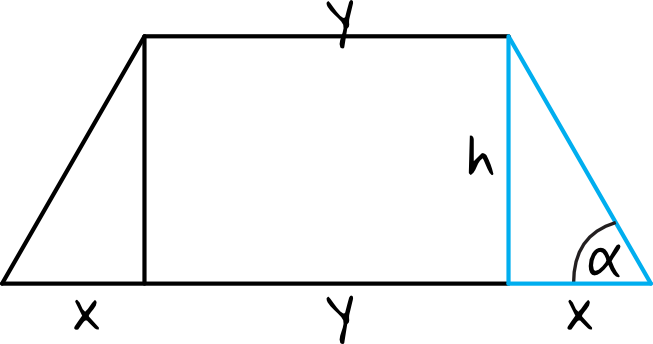
Zwróć uwagę na to, że powstał nam trójkąt prostokątny, który tworzą kawałek dolnej podstawy, wysokość figury oraz ramię trapezu. To właśnie z tego trójkąta będziemy za chwilę korzystać obliczając interesujące nas długości boków.
Krok 2. Obliczenie wysokości trapezu.
Zanim skorzystamy z utworzonego trójkąta prostokątnego, to możemy obliczyć wysokość naszej figury. Korzystając ze wzoru na pole trapezu możemy zapisać, że:
$$P=\frac{1}{2}(a+b)\cdot h \\
80=\frac{1}{2}\cdot20\cdot h \\
80=10\cdot h \\
h=8$$
Krok 3. Obliczenie długości odcinka \(x\).
Spójrzmy teraz na nasz rysunek pomocniczy, a konkretniej na ten nasz kluczowy trójkąt prostokątny. Wiemy już, że boczna przyprostokątna ma długość \(h=8\). Wiemy też, że \(tgα=\frac{4}{3}\), a skoro tangens odpowiada za stosunek długości przyprostokątnych, to błyskawicznie wyliczymy długość odcinka oznaczonego jako \(x\):
$$tgα=\frac{h}{x} \\
\frac{4}{3}=\frac{8}{x}$$
Mnożąc na krzyż otrzymamy:
$$4\cdot x=3\cdot8 \\
4x=24 \\
x=6$$
Krok 4. Obliczenie długości podstaw trapezu.
Dolną podstawę opisaliśmy sobie jako \(a=2x+y\), natomiast górną jako \(b=y\). Skoro już wiemy, że \(x=6\), to tym samym w całym zapisie pojawi nam się już tylko jedna niewiadoma, bowiem dolną podstawę możemy już zapisać jako \(a=2\cdot6+y=12+y\).
Wiemy, że suma podstaw musi być równa \(20\), zatem powstaje nam do rozwiązania proste równanie:
$$12+y+y=20 \\
12+2y=20 \\
2y=8 \\
y=4$$
To oznacza, że dolna podstawa ma długość \(a=12+4=16\), a górna podstawa ma długość \(b=4\).