Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
W trapezie podstawy są względem siebie równoległe. Korzystając zatem z własności kątów naprzemianległych możemy stwierdzić, że jeżeli kąt \(CAB\) oznaczymy jako \(α\), to także kąt \(ACD\) będzie miał miarę równą \(α\). Możemy więc powiedzieć, że w trójkątach \(ABC\) oraz \(ACD\) dwie znane nam miary kątów są jednakowe (kąt prosty oraz \(α\)), zatem i trzecia miara tego kąta musi być jednakowa (możemy ją oznaczyć jako \(β\)). To oznacza, że powstanie nam taka oto sytuacja:
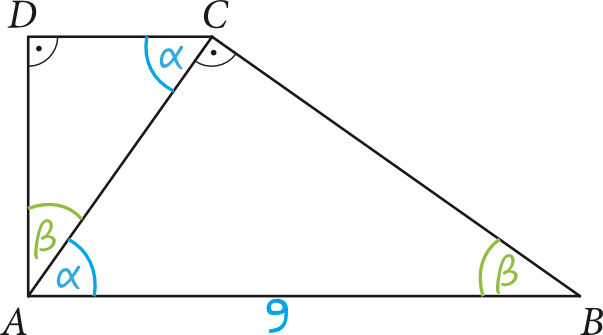
Krok 2. Obliczenie długości przekątnej \(AC\).
Z treści zadania wynika, że sinus kąta \(CAD\) (czyli naszego kąta β) jest równy \(\frac{\sqrt{3}}{3}\). Nie za bardzo wykorzystamy tę informację w trójkącie \(ACD\) (bo nie znamy choćby jednej długości boku tego trójkąta), ale możemy tę informację wykorzystać w trójkącie \(ABC\), wszak tutaj też jest kąt \(β\). Znamy długość przeciwprostokątnej tego trójkąta \(a=9\), zatem:
$$sinβ=\frac{|AC|}{|AB|} \\
\frac{\sqrt{3}}{3}=\frac{|AC|}{9} \\
|AC|=3\sqrt{3}$$
Krok 3. Obliczenie długości boku \(CD\).
Wracamy do naszego trójkąta \(ACD\). Znamy już długość przeciwprostokątnej tego trójkąta, bowiem \(|AC|=3\sqrt{3}\). Korzystając zatem z początkowej informacji o tym, że sinus kąta \(CAD\) jest równy \(\frac{\sqrt{3}}{3}\) możemy zapisać, że:
$$sinβ=\frac{|CD|}{|AC|} \\
\frac{\sqrt{3}}{3}=\frac{|CD|}{3\sqrt{3}} \\
|CD|=\frac{\sqrt{3}\cdot3\sqrt{3}}{3} \\
|CD|=\frac{9}{3} \\
|CD|=3$$
To oznacza, że górna podstawa ma długość \(b=3\).
Krok 4. Obliczenie wysokości \(AD\) (czyli wysokości trapezu).
Ponownie spoglądamy na mały trójkąt prostokątny \(ACD\). Znamy dwie długości w tym trójkącie, zatem i trzecią (będącą wysokością trapezu) bez problemu możemy policzyć, korzystając oczywiście z Twierdzenia Pitagorasa:
$$3^2+h^2=(3\sqrt{3})^2 \\
9+h^2=9\cdot3 \\
9+h^2=27 \\
h^2=18 \\
h=\sqrt{18} \quad\lor\quad h=-\sqrt{18}$$
Ujemny wynik oczywiście odrzucamy, bo długość nie może być ujemna, zatem zostaje nam \(h=\sqrt{18}\), co możemy jeszcze rozpisać jako \(h=\sqrt{9\cdot2}=3\sqrt{2}\).
Krok 5. Obliczenie pola trapezu.
Mamy już komplet informacji, znamy długości dwóch podstaw \(a=9\) oraz \(b=3\), znamy też wysokość trapezu \(h=3\sqrt{2}\), zatem:
$$P=\frac{1}{2}(a+b)\cdot h \\
P=\frac{1}{2}\cdot(9+3)\cdot3\sqrt{2} \\
P=\frac{1}{2}\cdot12\cdot3\sqrt{2} \\
P=6\cdot3\sqrt{2} \\
P=18\sqrt{2}$$