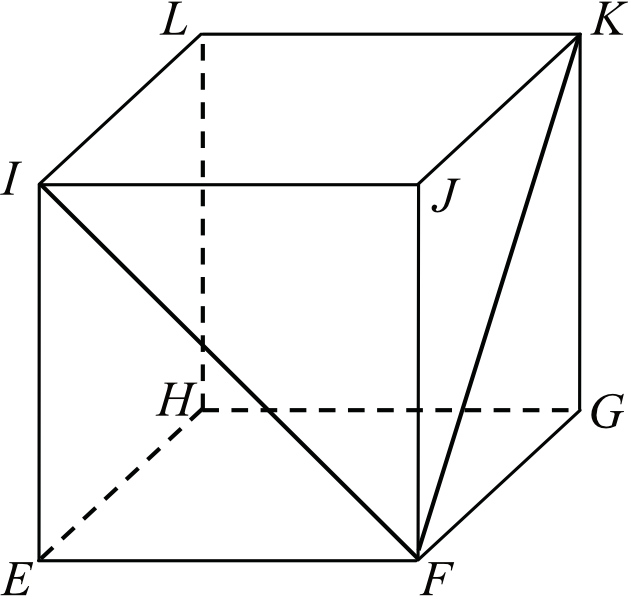
W sześcianie \(EFGHIJKL\) poprowadzono z wierzchołka \(F\) dwie przekątne sąsiednich ścian, \(FI\) oraz \(FK\) (zobacz rysunek). Miara kąta \(IFK\) jest równa:
\(30°\)
\(45°\)
\(60°\)
\(90°\)
Rozwiązanie:
Gdybyśmy połączyli ze sobą punkt \(I\) oraz \(K\) to otrzymalibyśmy trójkąt \(IKF\), którego jednym z kątów jest nasz poszukiwany \(\sphericalangle IFK\). Spróbujmy ustalić jaki będzie ten trójkąt \(IKF\). Wszystkie jego boku byłyby przekątnymi ścian, a skoro jest to sześcian, to każda z tych przekątnych miałaby tą samą długość. To oznacza, że trójkąt \(IKF\) jest równoboczny, a skoro tak, to \(|\sphericalangle IFK|=60°\).
Odpowiedź:
C. \(60°\)

